Final Exam With Answers

[You may omit any complete question or questions for 20%. This does not apply to individual sections within a question]

 Mean: 76.8/110
Standard Deviation: 14.2

I. Pick one of the following games, represent it in one of the ways we have discussed, such as a matrix or a tree, and describe a solution, explaining what solution concept you are using: (10 points)

1. Scissors/Paper/Stone: Matrix

	Player 1
Player 2		Scissors	Paper	Stone
	Scissors	0	(-1,1)	(1,-1)
	Paper	(1,-1)	0	(-1,1)
	Stone	(-1,1)	(1,-1)	0

The Von-Neumann solution is for each player to randomly choose one of the three strategies with equal probability, each time.

2. The Putting to Bed Game (your daughter says she will throw a tantrum if you don’t let her stay up during your dinner party)

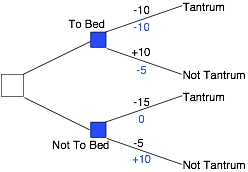
Subgame perfect equilibrium implies that you will put her to bed and she will not throw a tantrum. The argument is that once you do put her to bed, her payoff is higher if she doesn’t throw a tantrum, so she won’t. That implies that your payoff putting her to bed is higher than not putting her to bed.

I offer no guarantee that this solution accurately predicts what will happen.

3. Prisoner’s Dilemma: The numbers represent the size of the penalty, so larger numbers are worse.

		Baxter
		Confess	Deny
Chester	Confess	10,10	0,15
	Deny	15,0	1,1

The solution is for both to confess. It is a dominant solution—whatever one player does, confess is better than deny for the other.

(Surprisingly, several students gave matrices for which there was no dominant solution, since what it paid one player to do depended on what the other did.)

II. Apple and Motorola are agreeing on a joint project to introduce a new line of computers. The machines will be manufactured and sold by Apple using a new central processing unit (the chip that is the "brain" of the computer) that will be designed and manufactured by Motorola. In drawing up the contract, they must decide how to allocate various risks--that the chip will not turn out to be as fast as they expect or will cost more to produce, that the machines will not sell as well as they expect, etc. What considerations should determine which firm bears which risks, and why? (10 points)

Ideally, each party to the contract should pay the costs and receive the benefits of decisions that it controls and of outcomes it can better predict. The former rule reduces moral hazard, the latter reduces adverse selection.

In this case, Motorola should be responsible for the cost of risks associated with the production of the chip, since it controls the design and production and has more information about those risks than Apple does. Apple should be responsible for risks associated with the sale of the machines, since it is designing, producing and marketing the machines. One could get this result by having Motorola agree to a penalty if the chips end up slower, available later, or costing more than specified in the original contract, and having Apple agree to purchase a specified number of the chips, with a penalty if it chooses to purchase fewer.

A further rule in allocating risks is to allocate them to the party that is in the best position to spread risks, but it isn’t clear that the two firms differ in that respect here.

III. Six months from now your firm’s accountants will make their report, after which there will be a stockholder’s meeting and an attempt to have you removed as CEO. What things might you do between now and then to make the accounts look better and so keep your well paid job? (10 points)

Some relevant facts: The firm, which has been in business for fifty years and owns considerable amounts of land and real estate, has developed several products which are now leading brands in their fields. Recently, however, it has been the target of two class action law suits on different issues; your attornies believe one has a somewhat better than even chance of succeeding, one a slightly less than even chance.

Six months probably isn’t long enough to substantially improve the firm’s actual performance, but it is long enough to make the accounts look better. Some ways of doing so:

1. Sell assets, such as land, whose market value is much more than the value at which they are currently shown in the firm’s balance sheet—the latter being their purchase price long ago. If you are using the land, sell it and then rent it back.

2. For accounting purposes, the law suit with a better than even chance of succeeding counts as a liability of the estimated damage payment if it succeeds. You can improve the books by settling that for something less than that payment. The other suit doesn’t count as a liability at all, so don’t settle it.

3. The brand names of the products the firm developed are not assets for accounting purposes, so selling them—and, if necessary, licensing them back—will improve the balance sheet.

IV. Briefly explain one of the following three theoretical ideas, and give one example of its relevance to some legal question: (10 points)

A. Coase’s explanation of why firms exist

Firms exist because there are costs to market transactions; where it is less expensive to coordinate via hierarchal authority than via the market, it pays to put both parties being coordinated within a single firm. One example would be where there are substantial externalities from one actor to another—the benefit to a restaurant in a shopping center of having a theater next to it that brings customers past its door. One could have negotiations between the two firms, but it might be more efficient for one of them to buy out the other, putting both theater and restaurant in the same firm.

This is relevant to the question of whether a merger is being done to increase efficiency, and should be permitted, or is being done to increase market share so as to allow the merged firm to make monopoly profits.

B. The Berle/Means view of large corporations with dispersed stock ownership

Since the individual stockholder has little incentive to either know how well the firm is being run or do anything about it, the executive can largely ignore the interests of the stockholders in running the firm.

This is an argument against legal rules that make takeover bids more difficult, since takeover bids are one solution to the problem.

C. The Efficient Market Hypothesis

The price of a stock reflects all available information relevant to the value of the firm—where “available” has a range of possible meanings, depending on how strong a form of the hypothesis is being considered.

One implication of the intermediate version of the hypothesis, where “available information” means “public information,” is that false statements by the firm result in an incorrect price for its stock, which can be viewed as “fraud on the market.”

V. Your company's performance anti-correlates with the market--when most stocks go up, yours goes down, and vice versa. What can you say about the return you will have to offer investors in order to get them to invest in your firm? Explain. (5 points)

You should be able to get capital at a lower return than most other firms, including ones that can offer risk free returns, since your stock can be combined with the stock of companies whose risk correlates with the market, allowing purchasers to get the high returns on such stock while eliminating part of the risk.

VI. Answer one of: (10 points)

A. What is consumer surplus? Explain briefly.

Consumer surplus is the difference between what a consumer has to pay for the goods he buys and the highest price he would be willing to pay for them. It thus represents the net benefit to him of being able to buy those goods at the price at which they are available.

B. From the standpoint of economics, what is wrong with monopoly?

The price at which a monopoly maximizes its profits is above its marginal cost, with the result that potential customers who value the product at more than its cost of production but less than its price don’t buy them. That results in a lower net benefit to all concerned—firm + customers—than if the goods were sold at marginal cost, hence a dead-weight cost of monopoly.

A further problem is that the opportunity to become a monopoly may result in rent seeking expenditures.

C. What is economic efficiency?

Economic efficiency is a measure of net benefit to all concerned, measured by willingness to pay. A change improves efficiency if the total amount that those benefitted by the change would be willing to pay to get it is larger than the total that those worsened by it would be willing to pay to prevent it.

VII. What is an externality? Why are externalities a problem? Briefly discuss alternative ways of dealing with the problem. (10 points)

An externality is a cost or benefit that one actor imposes upon another, without requiring the consent of the latter.

It is a problem because the actor imposing a negative externality has no reason to include its cost in his decision of what actions to take, so may take actions which produce a net benefit for him but a net cost for him plus the others affected, reducing economic efficiency. Similarly, in the case of a positive externality, an actor may fail to take an action that would produce net benefits because it has net costs to him.

One solution is for the government to tell individuals what actions to take, on the basis of its calculation of net costs and benefits—as when the EPA requires a power plant to filter out some of the carbon from its emissions, or when auto makers are required to have catalytic converters in their cars. This depends on the regulator having the knowledge and incentives that lead to its giving the right orders.

A second solution is a “pigouvian tax.” The person who produces an externality such as air pollution is charged an amount that represents an estimate of the cost the externality imposes on others. He then has an incentive to take that cost into account in deciding what to do. The workability of this depends on the government having the knowledge and incentives to set the right taxes, and imposing the cost on the right party—the one who can at lower cost prevent it.

A third solution, along Coasian lines, is to define who has what rights and then let parties transact among themselves. If my air pollution imposes costs on my downwind neighbors larger than the cost to me of preventing it but the legal system gives me the right to pollute, they can buy that right from me. If the costs of the pollution are lower than the costs of preventing it but the legal system gives them the right to be free from pollution, I can buy the right from them. The effectiveness of this solution is limited by transaction costs that may prevent efficient transactions of this sort from happening.

VIII. Suppose drivers are strictly liable for damage to pedestrians. How does that affect the incentives of drivers to avoid accidents? Of pedestrians to avoid being the victim of accidents? Compare to the result under a negligence rule. How are your conclusions affected if some precautions drivers might take are unobservable? (10 points)

With strict liability, drivers bear all the cost of accidents, so have an incentive to take any precautions whose benefit in reduced accident costs are larger than their costs. Pedestrians bear no costs—this assumes that strict liability really compensates them fully—so have no incentive to take precautions.

Under a negligence rule, drivers are liable if they did not take all cost-justified precaution, so have an incentive to do so. Pedestrians expect that drivers will take all cost-justified precautions, so will not be liable, so pedestrians will expect to bear their own costs giving them an incentive to take all cost-justified precautions.

If, however, some driver precautions are not observable by the court which is deciding whether they were negligent, drivers have an incentive to take the efficient level of the observable precautions but to ignore costs to pedestrians in deciding what level of the unobservable precautions to take.

IX. You have been keeping track of what grade of gasoline you buy and what mileage you get and have used the data to calculate the correlation between octane rating and miles per gallon. The correlation coefficient is .8. What does this tell you about the relation between octane rating and mileage? You observe that 80 octane gasoline costs $2/gallon, 90 octane costs $2.10. Does that plus the correlation coefficient tell you which you should buy? Explain. Are there other ways of analyzing the data that would help? Explain. (10 points)

The correlation coefficient tells you that the relation between octane rating and mileage is close to linear, but does not tell you the slope of the line, so you have no idea how much improvement in mileage you would get from the higher octane so do not know if it is worth the price.

A linear regression, on the other hand, provides a regression coefficient which is an estimate of the slope of the line, information that would tell you which grade of gasoline would give you the most miles per dollar.

X. What does it mean to describe a result as “statistically significant?” (5 points)

It means that if the null hypothesis were true, it is unlikely that the result would have produced evidence that strong against it. If it is significant at the .05 level, for instance, that means that if the null hypothesis were true—if, for instance, the coin whose flips you were observing were a fair coin—the probability that the result would have been at least as far as it was in the direction predicted by the (alternative) hypothesis you are testing is no more than .05.

XI. What sort of information is provided by (answer all): (10 points)

Correlation coefficient

How close to linear the relation is between the two variables, and whether the slope of the line is positive or negative.

R²

What fraction of the variation of the dependent variable from its mean is explained by the regression. R²=1 would mean that the regression perfectly predicted the values of the dependent variable, R²=0 would mean that it did no better than predicting that the dependent variable would always be at its average value.

Z

How many standard deviations from the mean the result is. If the distribution is normal, a z table will tell you how likely it is to get a result at least that far from the mean in that direction.

t

How far a regression coefficient is from zero, relative to the standard error of the coefficient. A t table can then tell you how likely it is that you would have gotten at least that large a value of the coefficient by chance if the true value were zero.

Standard deviation

A measure of how much the variable varies. More precisely, the square root of the average squared deviation of the variable from its average.

XII. A friend casually remarks that the part time students at SCU are better qualified than the full time students, as shown by their LSAT scores. You suspect that he is mistaken. To check, you ask the records office for the average LSAT of all students and the standard deviation; to your surprise they provide the information. The average is 158, the standard deviation is 4. You poll the sixteen part time students in the evening class that you (and your friend) are taking, and discover that their average LSAT is 159. Calculate the corresponding z value. How likely is it that the evidence in favor of your friend’s claim would be this good if the claim itself was false—if the difference was merely due to sampling error? Is this a one tailed or two tailed test? Explain. The z table from the text is shown below. (10 points)

The standard deviation of the mean of n observations is the standard deviation of one observation divided by the square root of n, so in this case the standard deviation of the mean of 16 observations is 4/4 =1. Hence z is (159-158)/1 =1. Checking the z table, you see that the probability of z<1 is about .84, hence that the probability of getting evidence this for your friend’s claim by chance is about .16, so it isn’t very good evidence for the claim.

This is a one tailed test, since the claim was that the part time students were better qualified, not that they were either better or worse qualified.

What problems might occur to you or your friend with this approach to testing his claim?

The students are all from one class, so not a random sample—the class might be one that appealed to particularly strong or particularly weak students. Your information was gotten by asking the students, and they may have an incentive to overstate their LSAT scores.

END OF EXAM