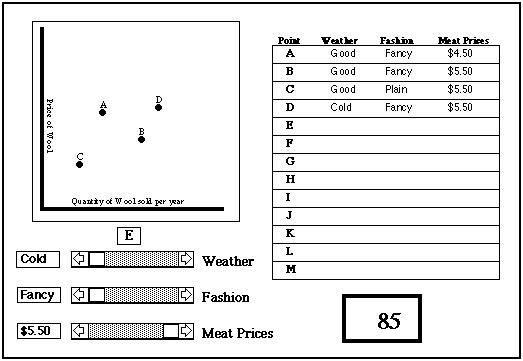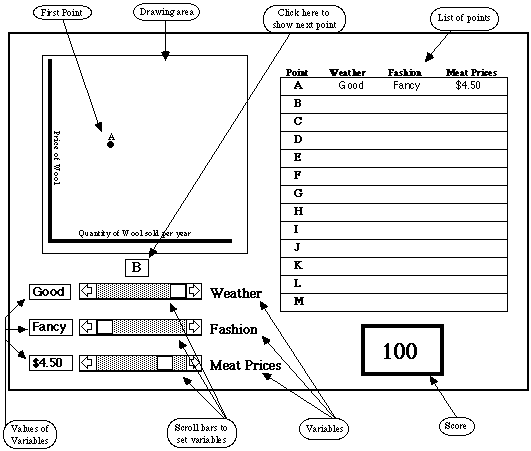
The next figure shows the screen after the student has just set his fourth point, D. The list of points shows the values for points A-D; the points themselves are shown on the drawing area. Note that the button above the scroll bars for the variables is labelled E, since clicking on it will draw the next point. If the student clicked E without changing the values of any of the variables, E would appear on top of D.
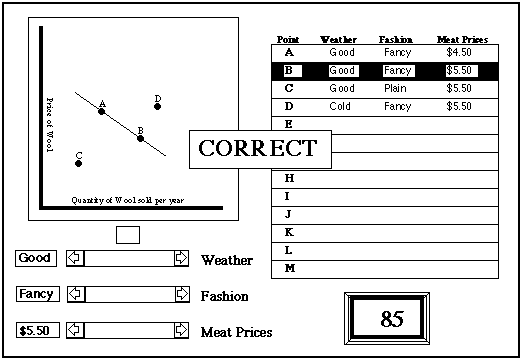
When the student believes that he has enough points (or when he has done as many as the program permits), he draws a supply curve and a demand curve, specifying the values of the variables for which each applies. The drawing is done with a mouse (Macintosh version); the specifying is done by clicking on the line on the list of values corresponding to one of his points. The program tells him if he is correct. If not, and if he has not used the maximum permitted number of points, he may get additional points before trying again. Each incorrect try lowers his score by 10 points. The figure below shows the screen just after the student has correctly drawn the demand curve corresponding to point B.
When the student has either successfully drawn a supply curve and a demand curve or used up all his points and given up, he is given a score (higher the fewer points used and the fewer wrong tries&endash;0 if he never gets either curve right) and an opportunity to watch a "replay."
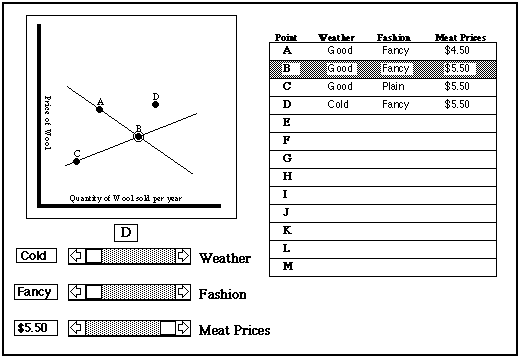
The replay starts with the values of the variables corresponding to point A. This time, the supply and demand curve are shown on the screen, along with their intersection (at point A). If the student clicks on any other point (either a labelled point or the corresponding line in the list of values) the screen shows the supply and demand curves for that point. The figure below shows the situation after the student has clicked on point B.
Bells and Whistles
There are several additional features that might be added. So far I have assumed that supply and demand curves are straight lines. The student could be given the option of permitting the program to use smooth curves as well.
A more interesting change would be to permit supply and demand curves to be influenced by additional factors not controlled by the student. The simplest way would be to add a small random term. The student, in drawing the curve, would be engaged not in rigorous deduction but statistical inference&endash;although the random term would be small enough so that the statistics could be done by eye. Alternatively, one might add an additional variable which the student could observe but not control, and which would vary randomly. If so, the variable should affect supply or demand but not both; that way a clever student could find one set of curves and use that knowledge in approximating the other.
A student selecting either of these "higher level" versions would start with a larger number of points and thus get a higher score for any given number of points chosen and errors made.
In my description so far, I have considered only one good, wool. The program should have a built-in list of ten or twenty goods, each with its corresponding variables and each variable with its corresponding list of possible values. The player starts by choosing a good, probably by scrolling through a list and double clicking on one; alternatively the program might choose one for him at random. In any case, the parameters of the actual curves should be chosen randomly each time the game is played.
I have assumed that the number of points the player is permitted to choose is limited to the number that will fit on the on-screen list. Alternatively, the list could be scrollable, permitting an unlimited number of points. One argument against this is that with more than a dozen or so points the drawing area may get pretty crowded.
There are a number of details of the program that I have not described, such as how the student tells the program that he is ready to draw curves. That might be a menu choice or an on-screen button. I have not described how the student actually draws a curve. If all curves are straight lines, one could use something like the line-drawing tool in MacDraw, which allows you to draw a line with the mouse and then move its end points around until it is properly located.
Mathematics
The underlying mathematics of the program are simple. We have a supply curve:
Qs=As+Bs*P
And a demand curve:
Qd=Ad-Bd*P
Each time the program is run or a new commodity is selected, values are randomly chosen for the parameters of the curves. In addition, the parameters are functions of the variables, with (as mentioned above) the supply parameters depending on one variable, the demand parameters on another, and a third variable entering one or both sets. All values of the parameters must obey the conditions:
1<Bs<5; 1<Bd<5 Condition 1
(200-200*Bs)<As<0; 200<Ad<200*Bd Condition 2
Ad/Bd>-As/Bs; (Ad-200)/Bd<(200-As)/Bs Condition 3
Here the units for price and quantity are pixels; the drawing area is assumed to be 200x200, roughly corresponding to the figures. Conditions 1 and 2 guarantee that the supply and demand curves will be entirely in the drawing area&endash;or in other words, that if Q is between 0 and 200 so is P. Condition 3 guarantees that the demand curve is above the supply curve for Q=0 and below for Q_=200, and thus that the two intersect for some 0<Q<200.
Once the parameters are determined (by an initial random procedure plus the effect of the values choosen for the variables) the program solves for Qs=Qd to find the point.
Arbitrage game
There exist net supply curves Sij for trading any pair of goods i,j. Student starts with fixed amount of a good, tries to increase his holdings by arbitrage. Ideally, 2 or more students play at once; best arbitrageur finds the opportunities first and eliminates them while profiting from them.
The Lesson
Goods exchange for other goods; at any instant there is a price at which good i can be exchanged for good j. These prices tend to be consistent; if one unit of i trades for two units of j, and one unit of j trades for 3 of k, then one unit of i will trade for about six units of k (pik@pijpjk).
One reason for the consistency is that if the prices are not consistent (pik pijpjk) it is possible for someone to profit by a series of trades in which he goes one direction (say from i to k) indirectly (exchanges i for j and then j for k) and the other direction directly (exchanges k for i), ending up with more of his initial good (i) than he started with. One effect of such trades is to bid the low prices up and the high prices down, moving the set of prices towards consistency.
The purpose of the program is to allow students to see how this mechanism works by themselves engaging in such trades (arbitrage).
The Program
There are two forms for the program, both of which will be described. The essential difference between them is in the equations determining prices. Either form may be played in either a one player or multiple player version; in the former the computer simulates the effect of additional arbitrageurs. The multiple player version could be played either on one machine or on several machines attached to a network. It should probably be designed for one machine and a network version created later if it looks as though networks are becoming sufficiently common to justify it. I will describe only the one machine version.
Single Player
There are five goods, hence ten prices (5x4/2). At the beginning, the program shows all ten prices and the amount of one commodity that the player starts with. Each turn the player trades some or all of what he has for one or more of the other goods; once the game has been going for a while he may have stocks of any or all of the five goods. Units acquired in one turn cannot be traded again until the next.
Each turn, there is a new set of prices. The player chooses what trades to make; his stock of commodities is altered accordingly. After a fixed number of turns, the game ends. All stocks of any good he holds other than the good he started with are converted into that good at the then prevailing prices. His score is the ratio of the amount of that good he then has to the amount he started with.
Multiple Player
In the multiple player version players move consecutively; prices are recalculated after every move. Players begin by choosing an initial bundle&endash;a given amount of a given commodity&endash;from alternative bundles offered by the program. The player who chooses last moves first.
Options
In a more advanced version, the player is managing an arbitrage fund, with specific objectives. If he choose to manage a low risk fund, the computer fires him if the value of his holdings drop by more than a stated percentage in any turn. If he manages a high risk fund, he is judged only be increase at the end. Other variants could be constructed.
New Ideas (1990)
1. Playing in real time. Repeated plays, computer reports cumulative average.
2. Player (or computer) chooses degree of risk aversion. Window shows utility as a function of income. If risk neutral, $1=1 utile. Again, computer reports cumulative average--this time utility as well as income.
3. Use currency, show a table of prices each way.
4. One can either have the underlying formula keep relative prices fixed, with random variation about that set of prices to introduce inconsistency, or one can allow relative prices to change substantially. In the second case, a player is exposed to substantial speculative risk. Diversification both allows safe arbitrage and reduces risk--sensible for risk averse players.
Mathematics
Version 1
In this version of the game, trades made by the players have no effect on prices; it corresponds to a situation in which the individual arbitrageur controls a negligable fraction of the goods on the market. Prices are set randomly each turn, with some tendency to move towards consistent values.
A simple way of modelling this would be for the program to randomly choose one good each turn, hold fixed the prices of the other goods in terms of that good, adjust all other prices towards consistency with those, then add in a random change to every price. The resulting equations, with i the good chosen randomly after turn t, would be:
, "j i
,"j,k i; j k
Here 0<a<1 is a parameter measuring the tendency towards consistency; the larger it is the more slowly inconsistencies in prices vanish. eij is a random variable.
Version 2
Underlying the game is a set of excess supply curves (quantity supplied minus quantity demanded as a function of price) representing net supply by non-arbitrageurs in each two good market. If, for instance, excess supply of oranges on the orange/apple market is -2 at a price of 1, that means that if one apple traded for one orange then the number of oranges offered by people who had oranges and wanted apples would be two fewer than the number of apples offered by people who wanted oranges and had apples. Since excess supply (including supply by arbitrageurs) must be zero at the equilibrium price (quantity supplied equals quantity demanded), price will be such as to make excess supply by non-arbitrageurs equal to demand by arbitrageurs.
Part of the point of this version of the game is that a player, by seeing and exploiting an opportunity to profit by arbitrage, eliminates or reduces that opportunity for other players or himself on later moves. In order for this to be true, units sold in one turn must effect the market in future turns, either because some of them are stored and consumed later or because of intertemporal substitution.
In the simplest form, we have a single period of production and consumption during which there are multiple periods of arbitrage. On each of the ten markets (ij), we have
Here
is the quantity demanded by arbitrageurs (players) in period t on the ij market&endash;or in other words, the number of units of j which players exchange units of i for. Aij is what the price would be on the ij market if there were no trades by arbitrageurs.
Note that in this version of the game, the price faced by a player is a function of how much he wishes to trade. The interface, as described below, reflects this; as the player changes the amount of his planned trade the price he will get also changes.
Two additional complications could be added to the underlying model. One is a random element; instead of A having a fixed value, we have:
Aij(t+1)=Aij(t)+eij
where eij is a random variable.
The second addition is to allow multiple periods of production and consumption; from the standpoint of the players, what this means is that arbitrage only temporarily eliminates profits from future arbitrage. The corresponding equations would be:
or, in a fancier version,
Here b<1 measures the rate at which the effect of a trade falls off over time. Of course, one could include both random variation and multiple periods of production.
If the game is being played by a single player, we will want some mechanism built in that simulates the effect of other arbitrageurs. The simplest would be a tendency of prices to move back towards consistency along the lines discussed above under version 1.
I do not expect that the completed program would include all of the alternative sets of equations which I have described, although we may wish to provide some choice of level of difficulty. I do assume that, while designing the program, it is relatively easy to change the set of underlying equations, and that we would want to do some experimenting on how the feel of the game varied with different versions. We probably do want at least one form of what I have called version 1 and one form of version 2, and for each both single player and multiple player versions.
The Interface
At any instant, the screen should show the player how much he has of each good this turn and how much he will have of each good next turn if he executes the trades he has currently chosen. While the player is adjusting his trades on a particular market, the screen should show the price on that market. It would also be desirable for the program to provide a simple calculator function to make it easier for the player to plan trades.
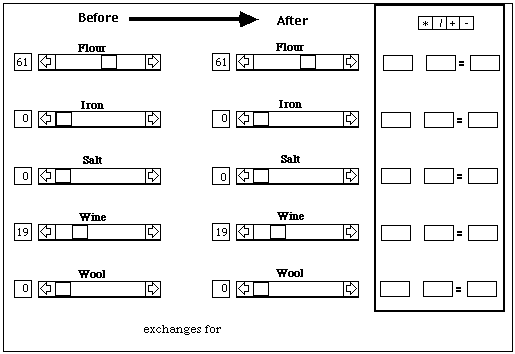
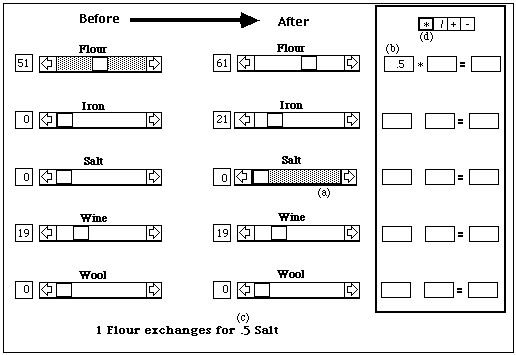
The figure shows the situation at the beginning of the player's move. He has 61 units of flour, 19 units of wine, and no iron, salt, or wool. Since he has not yet specified any trades, quantities after are the same as quantities before. Since he has not selected any good to trade, all of the scroll bars are blank, indicating that they are not active. Since he has not yet made any use of the calculator at the right of the screen, all of its boxes are blank.
The next figure shows the situation after the player has tentatively decided to trade 10 units of flour for iron. He selected flour by clicking on its scroll bar in the Before column, iron by clicking on its scroll bar in the After column. The bottom of the screen shows him the rate at which flour exchanges for iron. Moving the scroll box for flour 10 units left moved the scroll box for iron 21 units right, since 1 unit of flour exchanges for 2.1 units of iron.
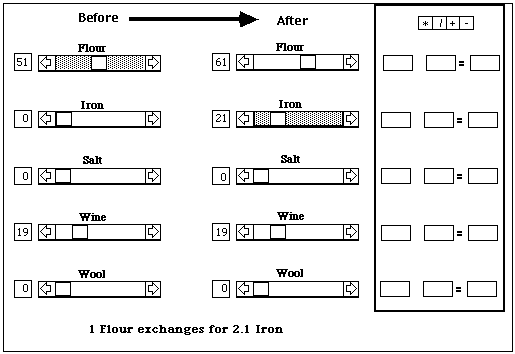
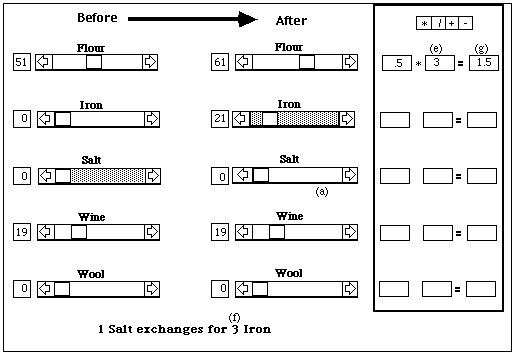
The next figure shows how the calculator is used. Suppose the player wishes to compare two alternative ways of getting iron from flour &endash;direct trade vs trading flour for salt and then salt for iron. He knows that the former method gives him 2.1 units of iron for each unit of flour. To find the return from the latter method, he first clicks on salt in the After column (a), then clicks on one of the left-hand boxes in the calculator region (b), then clicks on the number shown at the bottom of the screen as the rate at which flour exchanges for salt (.5) (c). Next he clicks the * icon at the top of the calculator box (d), to specify that he wants to multiply the two numbers that will be in the left and middle boxes of one of the rows of boxes on the calculator region; this is the point in the process illustrated in the figure below.
Next the student selects salt in the Before column and iron in the After column; the screen now shows at the bottom that 1 unit of salt exchanges for 3 units of iron. He clicks on the middle box of the calculator region (e). He next clicks on the number 3 at the bottom of the screen (f), which then appears in the middle box; the product of .5 and 3 appears in the right hand box of the calculator region (g), as shown in the next figure. The student observes that he is better off getting iron by the direct trade. If he is clever, he realizes that this means he can profit by trading flour for iron, iron for salt, and salt for flour.
Further Notes
In showing the interface, I have assumed a single set of five goods. It might be desirable to use those goods for what I have called version 2 of the program, and a set of currencies for version 1, thus distinguishing the two in the eyes of the students. It seems intuitively more plausible that one arbitrageur would influence the price of flour in a village than the price of marks on the international currency market.
Note that the exchange rate shown at the bottom of the screen (as in "1 Salt exchanges for 3 Iron") is a constant in version 1 of the program but varies slightly as the player varies the amount he plans to trade in version 2; in either case it shows the ratio of number of units received to number given up if he makes the trade currently selected.
It might be desirable to allow the student to display marginal revenue as well as price, since in version 2 they are not equal. Marginal revenue would be the increase in the number of units (say of iron) he gets as a result of giving up one more unit of (say) salt.
It would also be desirable to allow a student who has set up his trades for the turn and decides he does not like them to go back to the situation at the beginning of the turn; that might be a menu selection with a keyboard equivalent.
Strategies
The game, in all of its versions, permits three different strategies for winning. One strategy is pure speculation; the player acquires stocks of good that he expects to go up in relative price and gets rid of stocks of goods that he expects to go down. This strategy might work if the player either is lucky or takes advantage of the predictable element in price movements&endash;their tendency to move towards consistency.
The second strategy is pure arbitrage. To engage in pure arbitrage, the player first acquires stocks of at least three different goods. When the prices for those three goods are inconsistent he can, in a single turn, make simultaneous transactions on all three markets (ij, jk, ki) whose combined effect is to leave him with unambiguously more than he started with.
The third strategy is a mix of the two. A player with a stock of good i observes that the prices on the ijk market are inconsistent&endash;he could gain by trading i for j, j for k, and k for i. He trades units of i for j this turn. His plan is to trade j for k next turn and k for i the turn after. The problem with the plan is that the inconsistency will, on average, be decreasing over time, and in addition will have some random change in it.
Economics Note
I have implicitly assumed that, arbitrage aside, there is no connection between, say, the wool-steel market and the flour-steel market. An individual consumer/producer is interested in only two goods. Someone who trades wool for steel has nothing else to trade for steel and wants nothing else that wool can be traded for, so the price on that market is unaffected by prices on any of the other nine markets. This is obviously unrealistic, but greatly simplifies the modelling. One could construct a fancier set of equations to eliminate this assumption, but I doubt it is worth the trouble.
Alternative Interface: Four Currencies
In this version, everything is done by dragging piles of bills around the screen. When a pile is dropped in a different region, it converts and goes grey (assuming only one transaction is permitted per turn). Until the turn is over it can be dragged back. At the end of the turn, all dollars are combined into one pile, etc.
In any version, you can click on a stack, control z takes it back one step, shift control z takes it to where it started the turn. Shift click to select a bunch of stacks and do the same.
Alternative Games (1992 version)
1. One player, any number of trades. Each bill can only make one loop. There is a time limit within which to find the best trade. Everything ends up back as dollars.
2. One player, one trade per bill per turn. At the end of each turn, exchange rates are recalculated.
3. As in 2, but trades shift exchange rates towards consistency. Price shifts continuously as you trade; trades cannot be undone (save at new price).
4. As in 3, but relative prices are continually shifting (real time)
5. Multiple players, either consecutive (one machine) or simultaneous (network version). In the simple consecutive one, trades shift prices at the end of a player's turn, some randomness then added between turns. Alternatively, like 4. On the network, prices move continuously, trades cannot be undone.
Elasticity, TR, MR
Student draws a demand curve. Program shows elasticity at any point, shows TR and MR at request.
The Lesson
One of the things students learn about in Principles and Intermediate Microeconomics courses is elasticity. The elasticity of a demand curve is defined as minus the limit for small changes of the percentage change in quantity divided by the corresponding percentage change in price.
The purpose of this program is to give the student an intuitive feel for what elasticity is. It does so by letting him draw a demand curve and showing him the elasticity of that curve as a function of quantity. Ideally, the student should be able to modify the curve and watch how the elasticity is affected.
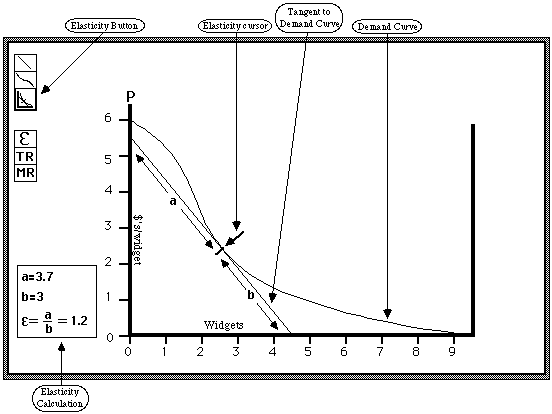
One of the reasons elasticity is important is that it is closely related to total revenue and marginal revenue. If total revenue is at a maximum then demand elasticity is one and marginal revenue zero. The program will also let the student view the total revenue and marginal revenue curves implied by his demand curve.
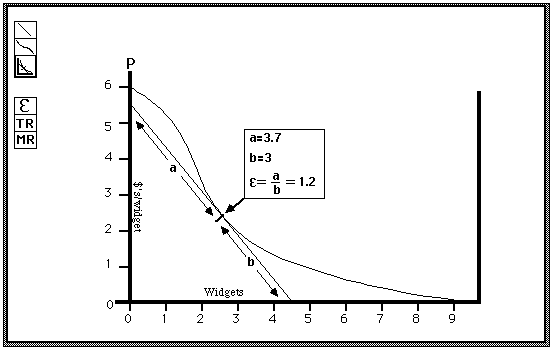
There is a simple geometric trick for calculating elasticity, discussed in my textbook and some others. The program will allow the student to see that the results of calculating it in that way are the same as those shown by the program.
In summary, the lesson of this program is a more intuitive understanding of the relation among a demand curve, its elasticity, and the total and marginal revenue functions it implies.
Program and Interface
I will describe two versions of the program, of which the second is better and harder to program. In the first version a demand curve is drawn but cannot be modified; if the student wants to look at a slightly different demand curve he starts over and draws it from scratch. In the second version the student can adjust the curve after it is drawn and watch the changes inelasticity, TR and MR.
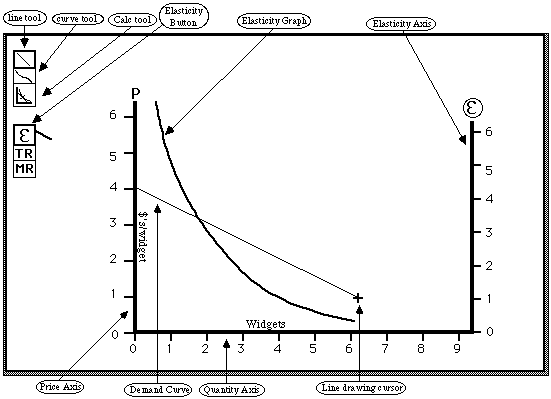
Version 1
The student is presented with a set of axes. The vertical axis shows price; the horizontal shows quantity. He selects either a straight line or a curve tool from a tool palette on screen and uses it to draw a demand curve. The straight line tool works like the line drawing tool in MacDraw or MacPaint. The curve drawing tool has a built-in smoothing feature to compensate for the usual shakiness of a mouse-drawn curve; the curve, instead of exactly following the cursor, grows towards the cursor, with the speed proportional to the distance between the cursor and the end of the curve.