In everything I have done so far, except for parts of Chapter 6, I assumed that trade involved many individuals or firms on each side. In deciding how much to sell or buy, the effect of the decision on the market price could be ignored, since the amount bought or sold by a single firm or individual would have a negligible effect on the price. While the demand curve faced by an entire industry was downward sloping (the more they sold, the lower the price), the demand curve faced by a single firm was essentially horizontal; similarly the supply curve faced by a single consumer was essentially horizontal even though the market supply curve was rising.
An example may make this clearer. If there were 100 identical firms in an industry, a doubling in the output of any single firm would cause total quantity supplied (by the industry) to increase by only 1 percent. The resulting fall in price would be even less than we would expect from applying a 1 percent increase in quantity to the demand curve, since as price falls, not only does quantity demanded increase, but quantity supplied (by the other 99 firms) also decreases. From the standpoint of the firm, the demand curve is almost perfectly elastic; changes in the quantity of output it produces have almost no effect on the price at which it can sell that output.
A firm in such a situation is sometimes described as a price taker. The firm takes the market price as given and assumes it can sell as much as it wants at that price. The firms described in Chapter 9 were price takers. The horizontal line that I drew at price in some of the figures of that chapter may be thought of as a (perfectly elastic) demand curve--the demand curve faced, not by the industry, but by the firm.
Not all industries consist of hundreds of firms. In this chapter and the next we will discuss situations where there are only a few firms in the industry, starting with the simple case of a monopoly--a firm that is the only seller of some particular good or service. In Part 1 of this chapter, we consider a monopoly that sells all of its output at the same price--a single-price monopoly. In Part 2, we consider a discriminating monopoly--a firm that sells different units of its output at different prices. In Part 3, we discuss reasons why monopolies might exist. In Part 4, we expand the discussion to include other small-numbers cases. In Chapter 11 we will go on to discuss strategic behavior and game theory, and to apply what we learn to the difficult problem of analyzing oligopoly--a market with several sellers.
We start with a monopoly that finds it must sell all of its output at the same price; the reasons why it must do so will be discussed later, when we consider the problems faced by firms that try to sell at different prices to different customers. Consider the widget firm whose situation is shown in Figure 10-1a. D is the total demand curve for widgets; since there is only one firm producing widgets, it is also the demand curve faced by that firm. MC is its marginal cost curve. The firm is producing at a quantity where MC = P, just as Chapter 9 says it should. Quantity is 20 widgets per month; price is $10/widget.
Suppose the firm reduces its output from 20 widgets to 19 widgets per month. Its production cost falls by about $9.50/month (the shaded area). Price rises to $11/widget. Before, its revenue was $200/month; now it is $209/month. Costs are down and revenue up, so its profit must have increased!
How can this be? Did we not prove in the previous chapter that profit was maximized at a quantity where P = MC? No. We proved that it was maximized at that quantity for a price-taking firm--a firm that could ignore the effect of its output on prices. If you go back to the relevant part of Chapter 9, you will see that we always took price as given.
The firm shown in Figure 10-1a is not a price taker but a price searcher. Rather than taking price as given and deciding how much to produce and sell at that price, it must decide how much to produce, knowing that by doing so it simultaneously determines both price and quantity--the more it produces, the lower the price.
When a price taker increases his output by one unit, he gains or loses according to whether the revenue from the additional unit is more or less than the cost of producing it. The revenue from one unit is the price it sells for, P, and the cost of producing one more unit is MC. So he gains if P > MC and loses if P < MC. As long as P > MC, his profit increases with each additional unit, so he keeps expanding his output until it reaches a level at which MC is equal to P, as described in Chapter 9.
For a price searcher, the situation is more complicated. When he increases his output, one of the effects is a reduction in the market price. Since (by assumption) all widgets are sold at the same price, this means that he gets a little less not only for the additional unit but also for each of the other units he is selling. His profit goes up by the price for which he sells the additional unit (P'), down by the cost of producing that unit (MC), and down by the initial quantity he was selling (Q) times the change in price (P - P'). The three terms are all shown on Figure 10-1b, for an increase in output from 20 widgets per month to 21. The increase in revenue--P' (times the additional number of units--1)--is shown darkly shaded. The decrease in revenue, 20(P - P'), is shown colored. The increased cost is the entire shaded area, light plus dark. The reduction in profit is the sum of the colored and the lightly shaded regions.
The effect of quantity on revenue and profit
for a price searcher. Figure 10-1a shows the effect of reducing
quantity from 20 to 19; Figure 10-1b shows the effect of increasing
quantity from 20 to 21. On Figure 10-1b, the decrease in revenue is
the colored area; the reduction in profit is that plus the lightly
shaded area.
Students are often puzzled as to why the firm must reduce its price on the "previous" units just to sell an "additional" unit. The mistake they are making is to think of "previous" and "additional" as referring to an actual sequence of events taking place in the market. They are imagining that the firm first sells 20 units and then sells 1 more; why should the latter event affect the former? But we are describing a firm that is either going to sell 20 units per month for the next ten years or 21 units per month for the next ten years and is trying to decide which alternative will yield higher profits. If it chooses to sell 21 units, it must sell them at a price at which consumers are willing to buy that many--which means a lower price than if it sells only 20. "Previous" and "additional" describe the order in which we think about the alternatives, not the order in which things actually happen.
To find out more exactly what the profit-maximizing quantity is for a single-price monopoly, we introduce a new concept--marginal revenue. Marginal revenue is defined as the increase in revenue per unit of increased quantity for very small changes in quantity, just as marginal cost was defined as the increase in cost per unit of increased quantity for very small changes in quantity. Students familiar with calculus may prefer to think of marginal revenue as the derivative of total revenue with regard to quantity, and marginal cost as the derivative of total cost with regard to quantity--calculus for the same thing.
If quantity is increased by one unit, revenue changes for two reasons. There is an increase in revenue of P' from selling one more unit, and there is a reduction in revenue of Q(P - P'). Here P and Q are the price and quantity before the increase, P' the price after. The change in price due to one additional unit is small compared to the total price--but in calculating the change in profit, the total price is only multiplied by one unit, while the change in price is multiplied by Q units. Figure 10-2a shows the two terms for an increase in output from 20 units to 21 units and shows marginal revenue as a function of quantity over a range of output. The shaded vertical rectangle is the gain from selling the additional unit; the colored horizontal rectangle is the loss from selling the other units at a lower price. Note that marginal revenue is always lower than price--by the lost revenue on the previous units due to the fall in price.
To express this with algebra instead of figures,
note that the change in price due to a one unit increase in quantity
is simply ![]() --the
slope of the demand curve. So we have:
--the
slope of the demand curve. So we have:
MR=P+Q(![]() )
)
On Figure 10-2a, the demand curve is a straight line. I drew it that way to illustrate a particularly simple way of finding a marginal revenue curve. It so happens that for a straight-line demand curve, marginal revenue is also a straight line, running from the vertical intercept of demand (the price at which quantity demanded is zero) to one half the horizontal intercept (half the quantity that would be demanded at a price of zero) as shown on the figure. This fact is of no significance at all for economics, since there is no reason to expect real-world demand curves to be straight lines, but it is very convenient for solving economics problems. Those of you familiar with calculus should be able to prove the result; it is quite easy. For those unfamiliar with calculus, it is almost the only thing in this book that you will find useful to learn without knowing why it is true; feel free to forget it as soon as the course is over.
Using marginal revenue to find the
profit-maximizing quantity. MR is the marginal revenue implied by
the demand curve D. Figure 10-2a shows how MR could be calculated.
Figure 10-2b shows the profit-maximizing quantity (Q)--where MR = MC.
P is the price at which that quantity will sell.
Now that we have a marginal revenue curve, maximizing the monopolist's profit is simple. If marginal revenue is higher than marginal cost, he should increase his output--the additional revenue (even allowing for the effect of the fall in price) is greater than the additional cost. If marginal revenue is lower than marginal cost, he should decrease output. If he has the correct (i.e., profit-maximizing) output, marginal revenue will be equal to marginal cost. This solution is shown on Figure 10-2b.
Note that we are solving for quantity and then using the demand curve to find the price at which that quantity will be sold. A mistake students often make in trying to solve this sort of problem is to confuse MR on the graph with P; they find quantity correctly at the intersection of MR and MC but then assume that the height of the point of intersection is the price. It is not; it is the marginal revenue. Price is the height of the demand curve at that quantity. Marginal revenue, marginal cost, and price are all in the same units (money divided by quantity--dollars per pound, for example, or pennies per gram), and they are all functions of quantity, so they can be and are shown as different curves on the same figure--but that does not mean that they are the same thing.
The profit-maximizing rule for a price searcher--"produce that quantity for which marginal revenue equals marginal cost"--is also the correct rule for a price taker. Since the impact of a change in quantity on price is zero for a price taker (that is why he is a price taker), marginal revenue is equal to price; each additional unit he produces increases his revenue by the price he sells it for. Since for the price taker MR and P are the same, MR = MC and P = MC are for him the same thing. The price taker producing where price equals marginal cost is a special case of the price searcher producing where marginal revenue equals marginal cost.
In our analysis of price-taking firms in Chapter 9, one of our main objectives was to find supply curves--first the supply curve of a firm and then the supply curve of an industry made up of many firms. We cannot do the same thing here. We cannot find the supply curve of a price searcher because a price searcher does not have a supply curve.
A supply curve tells how much a firm or industry will produce as a function of the price it can get for its goods. But the amount a price searcher produces does not depend only on the price it is getting but also on the price it could get at other levels of output. Its output depends not just on a price--the height of the demand curve at one point--but on the shape of the whole demand curve.
To see this, compare Figures 10-3a and 10-3b, which show two different demand curves and the marginal revenue curves they imply. Both figures also show the same marginal cost curve. The market price that the firm chooses to charge is the same in both cases--P--but the quantity is different. This demonstrates that even if we know the cost curves of the firm and the price, we cannot predict the quantity. So the supply curve, which shows quantity supplied as a function of price, does not exist.
Two different demand curves that imply the same
price but different quantities.
In deriving the supply curve of a firm from its cost curves in Chapter 9, the rule "produce a quantity for which MC = P" was only the first step. The second step was to observe that if profit was negative at that output, it could be increased by shutting down the firm and going out of business. This implies the additional rule "provided that at that quantity price is at least as high as average cost." That was why the supply curve was equal to the marginal cost curve only at and above its intersection with average cost.
The second rule applies to a monopoly as well; if the price for which the monopoly sells its products is less than its average cost, it would be better off going out of business. While the marginal revenue of a price searcher is different from that of a price taker, the average revenue is the same--price. If you are selling 1,000 apples at $0.50 each, your total revenue is $500 and your average revenue (total divided by quantity) is $0.50/apple--whether or not the amount you produce affects the price. So a different way of stating the rule is "Go out of business if average revenue is less than average cost."
The third step in deriving the supply curve for a price taker took us from the firm to the industry; as long as profit was positive, it would pay other firms to enter the industry. By doing so, they would drive down price and profit. The result was that in equilibrium, profit (revenue minus all costs) was zero.
In the case of a monopoly, the firm and the industry are the same; for one or another of several reasons discussed later in the chapter, no additional firms can enter. The argument for zero profit appears to vanish, leaving us with the possibility of monopoly profit--which will be discussed later, after we have looked at the different reasons why a monopoly might exist.
In several chapters, especially this one and Chapter 9, I have found it useful to describe curves--supply curves, demand curves, cost curves--as more or less flat. That is not an entirely adequate way of expressing the underlying idea; how flat a curve looks on a graph depends partly on how you choose to draw the vertical and horizontal scales. Figures 10-4a and 10-4b are graphs of the same demand curve (for water); the difference is that the horizontal axis shows gallons per day in Figure 10-4a and gallons per week in Figure 10-4b. To check that the graphs are really the same, note that at a price of $0.10/gallon, quantity demanded is 10 gallons per day (on Figure 10-4a) and 70 gallons per week (on Figure 10-4b). Yet the demand curve appears much flatter on Figure 10-4b than on Figure 10-4a. By changing the scale of the horizontal axis we have stretched the curve horizontally, making it look flatter.
The solution to this problem is to replace "flatness" with "elasticity." Elasticity was explained briefly in Chapter 7, but the idea was used there only in a qualitative way; very flat demand and supply curves were described as "very elastic," and very steep curves were described as "very inelastic." In discussing the behavior of a monopoly, we will require a somewhat more precise understanding of elasticity--as a quantitative, and not merely a qualitative, concept.
The elasticity of a demand (or supply) curve at
some quantity Q (remember that how flat a curve is may depend where
on it you are) is defined as the percentage change of quantity
divided by the percentage change of price, calculated for a very
small change in price. For those of you familiar with calculus, it is
![]() x P/Q. The
rest of you may think of it as the percentage change in quantity
resulting from a 1 percent change in price, or as P/Q divided by the
slope of the curve. Some economists include a minus sign in the
definition of demand elasticity so as to make both supply and demand
elasticity positive numbers (quantity demanded decreases when
price increases, so the percentage change in quantity is negative); I
will follow that convention.
x P/Q. The
rest of you may think of it as the percentage change in quantity
resulting from a 1 percent change in price, or as P/Q divided by the
slope of the curve. Some economists include a minus sign in the
definition of demand elasticity so as to make both supply and demand
elasticity positive numbers (quantity demanded decreases when
price increases, so the percentage change in quantity is negative); I
will follow that convention.
A highly elastic curve is one for which quantity changes a lot when price changes a little. A demand curve for which a price increase from $1.00 to $1.01 resulted in a decrease in quantity demanded from 100 widgets to 50 would be highly elastic; one for which a doubling of price caused only a 1 percent decrease in quantity demanded would be highly inelastic. One way of remembering this is to think about how much quantity demanded (or supplied) "stretches" when price changes--if the curve is very elastic, it stretches a lot. A unit elastic curve is one for which a 1 percent change in price results in a 1 percent change in quantity--elasticity equals 1. A curve is called elastic if its elasticity is more than that and inelastic if it is less. The elasticity of a curve typically varies along its length, so a supply curve may be elastic for one range of quantities, inelastic for another, and unit elastic at the point between the two ranges.
Two views of the same demand curve.
Quantity is measured in gallons per day on Figure 10-4a and in
gallons per week on Figure 10-4b. The same demand curve looks much
flatter on Figure 10-4b than on Figure 10-4a.
How flat a curve appears depends on how you draw it--changing the x axis from gallons per day to gallons per week flattens the curve considerably. This is not true of elasticity; if you change the units used to measure quantity by a factor of seven--as you do in going from gallons per day to gallons per week--both the quantity and the change in quantity are affected, but their ratio--the percentage change in quantity--remains the same. If a price drop of 1 percent causes you to increase your consumption of water by 10 percent, it does so whether consumption is measured in gallons per day or gallons per week. Elasticity is discussed further in the optional section of this chapter, where I show how to calculate it for various sorts of curves.
The concept of elasticity is useful in analyzing
the behavior of a single-price monopoly. If elasticity is 1.0 at some
point on a demand curve, that means that a 1 percent increase in
price causes a 1 percent decrease in quantity. Since revenue is price
times quantity, that means that where the demand curve is unit
elastic a small change in price or quantity has no effect on revenue.
The effect on revenue of an increase in price is just balanced by the
effect of the resulting decrease in quantity, so marginal revenue is
zero. A similar argument shows that where elasticity is greater than
1.0 (the elastic region of the demand curve), marginal revenue is
positive; where elasticity is less than 1.0, it is negative. More
generally, if we call the price elasticity of demand ![]() ,
we have:
,
we have:
![]()
The implications of this result for the relation between the elasticity of a demand curve and the behavior of a monopoly will be left as an exercise for the reader--in the form of problems at the end of this chapter.
So far, we have assumed that the monopolist sells all of his output at the same price. To see why he might prefer not to do so, we start with the simple case of a monopolist with 1,000 customers, all identical. We can represent the total demand curve by the demand curve of a single individual, remembering that for the total, all quantities are 1,000 times larger. Figure 10-5 shows such a demand curve. The firm, following the prescription of Part 1, sells the customer 6 cookies per week at a price of $0.70/cookie. At that quantity marginal revenue equals marginal cost; for simplicity I have made marginal cost constant.
Looking at the figure, we--and the president of the cookie company--make the following observation. Additional cookies cost $0.40 each to make. Up to a quantity of 12 cookies per week, additional cookies are worth more than $0.40 each to the customer (remember that a demand curve for an individual is also his marginal value curve). It seems a pity to lose those additional sales--and the money that could be made on them.
Discriminatory pricing in the cookie
industry--first try. The profit-maximizing single price is $0.
70/cookie. The firm charges each customer that price for the first 6
cookies but sells additional cookies for $0.50/cookie, increasing its
profit by the colored area.
As long as the firm must sell all cookies at the same price, there is no solution to this dilemma; in order to sell the customer more cookies, the firm must lower its price, and that would decrease, not increase, its profit. The cookie president gets an idea.
As a special favor to our customers, and in order to celebrate the tricentennial of the invention of the cookie, we are cutting our prices. For the first 6 cookies per week purchased by each customer, the old price of $0.70 remains in effect, but additional cookies may be purchased for only $0.50 each.
The result is shown on the figure. Each customer buys 10 cookies: 6 at $0.70 each and 4 more at the reduced price of $0.50. The customers are better off than before by the additional consumer surplus on the extra cookies (the gray area); the cookie company is better off by the profit on the additional cookies (the colored area). Since the additional 4 cookies cost $0.40 each to produce and are sold for $0.50, profit has increased by $0.40/customer/week (4 cookies x $0.10/cookie). With 1,000 customers, that comes to an additional $20,800/ year. The cookie president has reason to be proud of himself.
That is no reason to rest on his laurels. Figure 10-6a shows the more elaborate price schedule released for the next year. The first 6 cookies per week are still sold for $0.70 each, but the rest are now on a sliding scale--$0.65 for the seventh cookie, $0.60 for the eighth, $0.55 for the ninth, $0.50 for the tenth, $0.45 for the eleventh, and $0.40 for the twelfth cookie. The increased profit (compared with the original single-price scheme) is again thecolored area on the figure; as you can see, it has grown.
At this point, the cookie president's daughter, who took this course last year and has just joined the firm, enters the discussion. "Why," she asks, "should our customers get so much out of our business? We are the ones doing all the work, yet they end up with a large surplus--the gray area of Figure 10-6a. I don't mind losing the six little triangles--after all, they are entitled to a few crumbs--but surely we can do something about the big one." Figure 10-6b shows the pricing scheme she comes up with for the next year.
Figure 10-6b is very close to perfect discriminatory pricing--a price schedule that transfers all of the consumer surplus to the producer. Its imperfection--the "crumbs" referred to in the previous paragraph--comes from the problem of describing a discontinuous variable (3 cookies or 4 cookies but never 3.141532 cookies) with concepts, such as marginal value, more suited to continuous variables (water--or wine). It is possible, by setting the price schedule perfectly, to use such a set of prices to end up with all the surplus, crumbs included.
Discriminatory pricing in the cookie
industry--improved versions. On Figure 10-6a, cookies are sold on
a sliding scale starting at $0.70/cookie. On Figure 10-6b, the price
starts at $0.95/cookie and is $0.05 less for each additional cookie.
There is an easier way to do the same thing. The next year, the company announces a new and much simpler pricing policy. Cookies will no longer be sold to the general public--only to members of the cookie club. Members can buy cookies at cost--$0.40/cookie--and may buy as many as they wish at that price. The membership fee is $3.60/week. That, by a curious coincidence, is the total consumer surplus received by a consumer who is free to buy as many cookies as he wants at a price of $0.40/cookie. This two-part price (membership plus per-cookie charge) first maximizes the sum of consumer and producer surplus (by inducing the consumer to buy every cookie that is worth at least as much to him as it costs to produce) then transfers the entire consumer surplus to the producer.
Before I go on to more complicated cases, let us look a little more carefully at the result so far. The firm maximizes its profit by charging a price equal to marginal cost and an additional membership fee equal to the entire consumer surplus. The effect of selling at MC is to maximize the sum of consumer and producer surplus; Figures 10-7a through 10-7c show that the sum for a price higher than MC (Figure 10-7a) or lower than MC (Figure 10-7c) is lower than for a price equal to MC (Figure 10-7b). Note that the colored area in Figure 10-7c is a loss due to selling below cost; it is larger than the increase in the lightly shaded area (membership fee) resulting from the lower price. The overall effect of reducing price below marginal cost is to reduce the firm's profits by the difference--the darkly shaded (and colored) triangle.
The conclusion can be simply stated. The effect of the entrance fee is to transfer the consumer surplus to the producer, giving him the sum of both surpluses--which he maximizes by setting price equal to marginal cost. If you think this sounds familiar, you are right. It is the same argument that was used at the end of Chapter 4 to show why movie theaters should sell popcorn at cost. For more on that subject, stay tuned. It is also the pattern of pricing often used by sellers of telephone services, electricity, and a variety of other goods and services.
Two-part pricing--calculating the optimal price
and membership fee. Figure 10-7b shows the pattern that maximizes
the firm's profits; the price per cookie is equal to marginal cost,
and the membership fee is equal to the consumer surplus at that
price. Figures 10-7a and 10-7c show that a higher or lower price
results in less profit.
So far, we have assumed that all customers are identical; under those circumstances, the seller may achieve something quite close to perfect discriminatory pricing, although there are some difficulties which we shall discuss later. I shall now complicate the problem by assuming that there are two different kinds of customer with different demand curves. Type A customers have demand curve DA on Figure 10-8, which is the same as the demand curve shown on Figures 10-5 through 10-7; type B customers have demand curve DB. There are 500 customers of each type.
The cookie president and his daughter have a problem. If they continue their previous two-part pricing system ($0.40/cookie plus $3.60/week), customers of type A will continue to join the club and buy the cookies, but customers of type B, for whom the consumer surplus at $0.40/cookie is only $2.40/week, will find that the cookie club costs more than it is worth and refuse to join. If, on the other hand, the membership fee is reduced to $2.40/week (the consumer surplus for type B consumers), the cookie company will lose $1.20/week that it could have gotten from the type A customers at the higher price.
The revenue from selling cookies just covers the cost of producing them (since the per-cookie price is just equal to marginal cost), so whatever membership price the firm decides to charge, profit will be equal to the revenue from selling membership in the cookie club. At the higher price, that is $3.60 from each of 500 type A customers; at the lower price, it is $2.40 from each of 1,000 customers (both type A and type B). Profit is maximized by charging the lower price--while regretting the consumer surplus left, unavoidably, in the hands of the type A customers.
The case of nonidentical customers.
DA is the demand curve for type A customers; DB
is the demand curve for type B customers.
There are two ways in which the cookie president can try to improve on this result. One, which we will discuss later in this section, is to somehow figure out which customers are of which type and charge a higher membership fee to the type A customers--or rather, raise the membership fee to $3.60 and offer a "special discount membership" to the type B customers. The other is to raise the per-cookie price.
The reason he might raise the price can be explained verbally as follows: "At any price, type A customers eat more cookies. Hence raising the price is an indirect way of charging them more than the type B customers. The total surplus is reduced, for the reasons shown in Figures 10-7a through 10-7c, but since I am no longer receiving the total surplus, that is no longer a conclusive argument against raising price. The increase in my share of the surplus may outweigh the reduction in the total."
The argument can be made more precisely with the use of graphs. I will limit myself to showing that there is a combination of higher price per cookie and lower membership fee that results in a higher profit in this particular case; this is shown on Figures 10-9a and 10-9b. Our previous solution (membership of $2.40) gave a profit of $2,400/week. The new solution is a price of $0.50/cookie and a membership fee of $1.667. Revenue on memberships totals $1,667; profits on cookie sales ($0.10/cookie times number sold) are $1/week on each type A customer and $0.667/week on each type B customer. Total profit is $2,500/week--$100 more than with the previous solution.
This example demonstrates that in at least one case--the one I have just described--a monopoly can increase its profits by selling its product for more than marginal cost, even though it is in a position to charge a two-part price. The example does not demonstrate that it always, or even usually, pays a monopoly to do so. Alfred Marshall, who put together modern economics about 100 years ago, warned in an appendix to his Principles of Economics of the danger of deducing general principles from specific examples; it is always possible that in choosing the particular example you may, without realizing it, assume away one of the essential elements of the general problem. One should therefore, Marshall argued, base one's final conclusions not on examples but on proved theorems.
Price above marginal cost as a device for
discriminatory pricing. The firm is charging a price higher than
MC as an indirect way of charging more to type A customers (Figure
10-9a) than to type B customers (Figure 10-9b). The resulting profit
is higher than with P = MC.
We have finally found a possible solution to the popcorn puzzle. (I only kept you in suspense for eight chapters.) In my previous discussions, I assumed that the theater customers were all identical; if that assumption holds, so does the conclusion--that the theater should sell popcorn at marginal cost and make its profit on admission tickets. But if customers are not identical and if those who are willing to pay a high price for a ticket tend to be the same ones who buy a lot of popcorn, then the combination of cheap tickets and expensive popcorn may be an indirect way of charging a high admission price to those who are willing to pay it without driving away those who are not.
So far, most of the discriminatory pricing we have discussed was designed to charge different prices to the same person for different units consumed, thus taking advantage of the fact that the consumer has a higher marginal value for the first few units and will, if necessary, pay a higher price for them. This was done either by charging different prices for different units or by charging a two-part price--one price to buy anything and another for each unit bought. Only at the end of the previous section did we discuss attempts to discriminate between different customers, in the context either of a monopolist who knows exactly who has what demand curve and prices accordingly or one who uses a per-unit price higher than marginal cost as an indirect way of discriminating between high-demand and low-demand customers.
An alternative approach for the cookie company--or any monopolist selling to a diverse group of customers--is to try to find some indirect way of distinguishing between customers who are and are not willing to pay a high price. Discriminatory pricing of this sort is very common--so much so that some of us have gotten into the habit, whenever we see a pattern of behavior on the marketplace that does not seem to make sense, of trying to explain it in terms of price discrimination.
One familiar example is the policy of charging less for children than for adults at movie theaters. A child takes up just as much space as an adult--one seat--and may well impose higher costs, in noise and mess, on the theater and the other patrons. Why then do theaters often charge lower prices for children? The obvious answer is that children are (usually) poorer than adults; a price the theater can get adults to pay is likely to discourage children from coming--or parents with several children from bringing them.
A similar example is the youth fare that airlines used to offer. It was a low fare for a standby ticket, offered only to those under a certain age. The lower fare reflected in part the advantage to the airlines of using standby passengers to fill empty seats, but that does not explain the age limit. The obvious answer is that making the fare available to everyone might have resulted in a substantial number of customers "trading down"--buying a cheap standby ticket instead of an expensive regular one. Presumably the airlines thought that making it available to youths would result in their buying a cheap standby ticket on an airplane instead of taking the bus, driving, or hitching.
The same analysis that explains low fares for youths also explains special discounts for old people; they too are (often) poor. It also explains large price differences between "high-quality" and "low-quality" versions of the same product--hardcover books and paperbacks, first-class seats and tourist-class seats, and so on. The difference may merely reflect a difference in production cost--or it may be a device to extract as much consumer surplus as possible from those customers who are willing, if necessary, to pay a high price and are likely to prefer the luxury version of the product.
Another example of discriminatory pricing is the Book of the Month Club. A publisher who gives a special rate to a book club is getting customers most of whom would not otherwise have bought the book; since most of those who are willing to buy the book at the regular rate are not members of the club, he is only stealing a few sales from himself. Discount coupons and trading stamps in grocery stores may be another example. Customers with a high value for their own time do not bother with such things--and pay a higher price.
A firm engaged in this sort of discriminatory pricing faces two practical problems. The first is the problem of distinguishing customers who will buy the good at a high price from those who will not. In the examples I have given, that is done indirectly--by age, taste, membership in a discount book club, or the like. A more elegant solution is said to be used by optometrists. When the customer asks how much a new pair of glasses will cost, the optometrist replies, "Forty dollars." If the customer does not flinch, he adds "for the lenses." If the customer still does not flinch, he adds, "each." I use a similar technique in selling my services as a public speaker.
The second problem is preventing resale. It does no good to offer your product at a low price to poor customers if they then turn around and resell it to rich ones, thus depriving you of high price sales. This is why discriminatory pricing is so often observed with regard to goods that are consumed on the premises--transportation, movies, speeches, and the like. If GM sells cars at a high price to rich customers and at a low price to poor ones, Rockefeller can send his chauffeur to buy a car for him. There is little point in having the chauffeur take a trip for Rockefeller or see a movie for him.
The problem of controlling resale also exists with the form of discriminatory pricing discussed earlier in the context of identical customers--discriminating between what the customer is willing to pay for his first cookie and what he is willing to pay for his tenth. The problem occurs when a cookie club member buys 48 cookies per week, eats 12, and sells 36 to friends who have not paid for membership in the cookie club. That is why two-part (or more generally multipart) pricing is more practical with electricity or health spa services than with cookies.
The ability of a firm to engage in successful discriminatory pricing also depends on its being a price searcher--having some degree of what is sometimes called monopoly power. In a market with many firms producing virtually identical products, price discrimination is impractical; if one firm tries to sell the product at an especially high price to rich customers (or customers who very much want the product), another firm will find it in its interest to lure those customers away with a lower price. Airlines do not wish to have their own customers trade down to a cheaper ticket--but Delta has no objection to getting a customer to give up a first-class ticket on Pan Am in order to buy a tourist ticket on Delta.
All of the cases I have described involve some element of monopoly. Youth fares existed at a time when airline fares were controlled by the Civil Aeronautics Board (CAB), a regulatory agency that provided government enforcement for a private cartel, keeping rates up and new firms out; they have since disappeared along with airline regulation. Copyright laws (and the economics of publishing) give each book publisher a monopoly--not of books, or even of a particular type of book, but at least of a particular book. The result is that publishers are price searchers; each knows that some customers are willing, if necessary, to pay a high price, while others will only buy the book if they can get it at a low price. Movie theaters have an element of monopoly, at least in areas where they are scarce enough that a customer cannot conveniently pick among several showing the same film.
This brings me to the question of why monopolies exist--which is the subject of the next part of the chapter.
Why do monopolies exist? Under what circumstances will there be only one firm in an industry? Why, if revenue is greater than cost, do not other firms choose to start producing the same product?
One answer may be that if they do, the monopolist will call the police. The original meaning of monopoly was a government grant of the exclusive right to sell something. Typically such monopolies were either sold by the government as a way of raising money or given to people the government liked, such as the king's mistresses (or their relatives). Monopolies of this sort are still common. One obvious example is the Post Office--a monopoly that is not only protected by the government (the Private Express Statutes make competition illegal) but also run and subsidized by it.
A second possibility is a natural monopoly. This occurs when the shape of the firm's cost curve is such that a firm large enough to produce the total output of the industry can do so at a lower cost than could several smaller firms. Figure 10-10a shows an example of such a cost curve. A firm producing q1 at price P has positive profits (price is greater than average cost), but a firm producing q2 = q1/2 at the same price does not. If one large firm is formed and sells at P, smaller firms will not find it worth their while to enter the market.
Another case very similar to the natural monopoly is the natural cartel. A cartel is a group of firms acting together as if they were a single monopoly. Cartels are most likely to occur in industries where economies of scale (advantages that allow large firms to produce more cheaply than small ones) are not quite sufficient to allow one giant firm to produce more cheaply than several large ones; such an industry is likely to consist of a few large firms. Figure 10-10b shows the sort of cost curves that might lead to a cartel; what is important is not simply the shape of the cost curves but their relation to the market demand curve--the fact that minimum average cost occurs at a quantity that is a large fraction of the quantity demanded at a price equal to minimum average cost. This guarantees that any firm producing less than (in this example) about one third of the industry's total production will have higher average costs than larger firms and so be at a competitive disadvantage.
As long as the firms in a cartel cooperate with each other, the cartel functions like a natural monopoly. Some of the difficulties in maintaining such cooperation will be discussed in Chapter 11. One common solution is a government-enforced cartel, such as the U.S. airline industry prior to deregulation or the U.S. rail industry from the end of the nineteenth century to the present.
Cost curves for a natural monopoly (a) or
natural cartel (b). Figure 10-10a shows cost curves for which a
large firm producing the entire amount demanded has a cost advantage
over smaller firms. Figure 10-10b shows the case where a firm large
enough to produce a large fraction of total industry output has lower
costs than smaller firms.
Most people who think about natural monopolies imagine them as gigantic firms such as Bell Telephone or GM. It is widely believed that such firms, by taking advantage of mass production techniques, can produce more cheaply than any smaller firm; it has often been argued that, for this reason, free competition naturally leads to monopoly. As George Orwell put it, "The trouble with competitions is that somebody wins them."
This does not seem to be a correct description of the real world, at least at present. While there are advantages to mass production, in most industries a firm need not produce the entire world's output in order to take advantage of them. The steel industry, for example, produces in very large plants, but the largest firm (U.S. Steel) consists not of one gigantic steel mill but of over 100 large ones. A firm 1 percent of its size can operate one steel mill and take advantage of the same scale economies. The president of such a firm is closer to the worker pouring the steel by several layers of administration than is the president of U.S. Steel, which may be one reason that U.S. Steel has not, in recent decades, been one of the more successful firms in the industry.
Bell Telephone was until recently a government-enforced monopoly--it was illegal for another firm to try to compete by offering local phone service in an area served by Bell, or for Bell to compete in an area served by General Telephone or one of the smaller companies. GM is not a monopoly even within the U.S., and such limited monopoly power as it does have in the U.S. market is largely a result of tariffs that restrict the ability of foreign auto producers to compete with it.
I am a more typical example of a natural monopoly than is GM. As a public speaker, I produce a product that is, I believe, significantly different from that produced by anyone else; if you want a certain sort of talk on certain sorts of subjects, you must buy it from me. The result is that I am a price searcher. Some groups are willing to pay a high price for my services, some a lower price, some would like me to speak but can offer nothing but expenses and dinner. If I sell my speeches at a fixed price, I must either price some of the customers out of the market (even though I might enjoy speaking to them, and so be willing to do so for free--at some levels of output, my marginal cost is negative) or else accept low fees from some groups that are willing to pay high ones. In fact, I engage in a considerable amount of discriminatory pricing, offering free or low-cost speeches to especially worthy (i.e., poor) groups. The same is true of my services as a writer; I have one outlet that pays a very high rate, but I recently wrote a column on something that interested me for a new magazine that paid nothing.
My monopoly over the production of certain kinds of speeches and articles is a far more common sort of natural monopoly than that of Bell or GM; it is due not to the huge scale of production but to the specialized nature of the product. Examples of similar monopolies would be the only grocery store in a small town or your favorite thriller writer. It is not only a more common sort of monopoly, it is also one much more important to those of you who expect to be in business. It is unlikely that you will ever be the head of GM or U.S. Steel, and if you are, you may find that the monopoly power of those firms is very limited. It is much more likely that you will find yourself selling a specialized product in a particular geographical area, and so functioning as a price searcher facing a downward-sloped demand curve. It is even more likely that some of the firms you deal with will be in such a position. If so, the analysis of this chapter should help you understand why they sell their product in the way they do.
There is one more sort of monopoly worth discussing--the artificial monopoly. An artificial monopoly is a very large firm that has no advantage in production efficiency over smaller firms but nonetheless manages to drive all of its competitors out of business, remaining the sole producer in the industry. A typical example is the Standard Oil Trust--not the real Standard Oil Trust as it actually existed in the late nineteenth and early twentieth centuries but the Standard Oil Trust as it appears in many high school history books. In the optional section, I discuss that case along with the general problem of maintaining a monopoly position without either a natural monopoly or a government grant of monopoly power. My conclusion there is that the artificial monopoly is largely or entirely a work of fiction; it exists in history books and antitrust law but is and always has been rare or nonexistent in the real world, possibly because most of the tactics it is supposed to use to maintain its monopoly position do not work.
One important difference between an industry consisting of many firms and an industry consisting of one was mentioned earlier; in the former case, the equilibrium price is such as to make economic profit zero, since positive profits attract new firms and their output drives down the price. This is not the case for a monopoly industry. If it is a government-granted monopoly, new firms are forbidden by law; if it is a natural monopoly, there is only room for one firm.
The result is monopoly profit. If the government simply sells the right to be a monopoly to the highest bidder, the price should equal the full monopoly profit that the winner expects to make; if he had bid less, someone else would have outbid him. In this case, the monopoly firm makes no net profit, since its costs include what it paid to become a monopoly. What would have been monopoly profit all goes to the government. If instead of selling the monopoly privilege, the government gives it away, then the firm receives the monopoly profit--unless "giving away" really means selling for something other than money paid to the government. Examples might be the attentions of the King's mistress (old style) or discreet contributions to the re-election fund of the incumbent president (new style).
In the case of a natural monopoly, the situation is more complicated. Since the monopoly is not created by the government, there is no reason to expect the government to control who is the monopolist. Once a firm has the monopoly, it may be able to earn substantial monopoly profits without attracting competitors. A competitor would have to duplicate the initial firm's productive facilities, making the industry's capacity twice what it could sell at the price the existing monopoly was charging; the resulting price war might well hurt both firms, a possibility that may persuade the second firm not to try to enter the market.
This raises the question of how the first firm got its monopoly position in the first place. That question is discussed in Chapter 16, where it is shown that under at least some circumstances, the zero-profit condition does apply to natural monopolies, with the monopoly profit being competed away in the process of obtaining it.
So far we have considered only one kind of price searcher--a monopoly, the only seller of a good or service. Our next step is to consider its mirror image. Having done so, we will go on to discuss briefly some harder cases.
I began this chapter by dropping the assumption that individuals can sell and buy as much as they like without affecting the price. So far, I have discussed monopolies--individuals and firms that are the only sellers of some good or service. An individual or firm that is the only buyer of a good or service is called a monopsony. An example might be the one large employer in a small town (a monopsony buyer of labor) or the DeBeers diamond cartel (a monopsony buyer of rough diamonds).
Just as a monopoly must consider how much its revenue from selling widgets increases when it sells one more widget, so a monopsony must consider how much its expenditure for widgets increases when it buys one more widget. A monopoly's marginal revenue is less than the price it sells its goods for because, in order to sell more, it must lower its price. A monopsony's marginal expenditure is more than the price it pays for each widget, because by buying more it bids up the price--not only for the additional widget but for all other widgets it buys.
A firm that buys its inputs in a competitive market buys that quantity for which price equals marginal revenue product, as we saw in Chapter 9. At any other quantity it could increase its profit by buying more (if MRP>P) or less (if MRP<P). A monopsony, by exactly the same argument, buys that quantity for which marginal expenditure equals marginal revenue product. Since marginal expenditure for a monopsony is higher than price, it will generally use less of the input of which it has a monopsony than if it were a price taker.
The monopsony's behavior is exactly analogous to that of a monopoly. The monopoly sells the quantity for which marginal revenue equals marginal cost, and thus sells less than if it were selling in a competitive market. The monopsony buys the quantity for which marginal expenditure equals marginal revenue product, and thus buys less than if it were buying in a competitive market. If you convert the monopoly into a competitor, its marginal revenue becomes equal to the price at which it sells its goods and we are back with P=MC as in Chapter 9. If you convert the monopsony into a competitor, its marginal expenditure becomes the price for which it buys its input, and we are again back in Chapter 9 with P=MRP.
Figure 10-11 shows the result graphically. S is the supply curve for a good whose only purchaser is a monopsony. ME is the monopsony's marginal expenditure--the amount by which its expenditure on the input increases if it buys one more unit. The monopsony buys a quantity Qm for which ME=MRP. If it behaved like a firm buying in a competitive market it would instead buy Qc, the quantity where MRP crosses S and is thus equal to the price.
Using marginal expenditure to calculate the
quantity of an input purchased by a monopsony. The monopsony,
which uses onions as an input, purchases the quantity (Qm)
for which marginal expenditure on onions equals the marginal revenue
product of onions. The price of onions is Pm, the price at
which that quantity is supplied by onion producers, as shown by the
supply curve S. A competitive firm would have purchased Qc
at price Pc.
A market can have any number of buyers and any number of sellers. Most of my analysis so far has concentrated on the case of many buyers and many sellers; in this chapter, I have considered the cases of one seller and many buyers (monopoly) and one buyer and many sellers (monopsony). These are the easy cases, the ones for which economics gives relatively simple and straightforward solutions. The hard problems are the cases of oligopoly (several sellers and many buyers); oligopsony (several buyers and many sellers); bilateral monopoly (one buyer, one seller); bilateral oligopoly (several sellers, several buyers); one seller, several buyers (no name I know of); and one buyer, several sellers (ditto).
What all of these hard cases have in common is strategic behavior. In all of the analysis so far, except for the discussion of bilateral monopoly in Chapter 6, the individual or firm could decide what to do while taking what everyone else was doing as given. That is appropriate in a price taker's market; since my output is a negligible part of total output, it is not in the interest of any of my customers to say to me, "I want what you are selling at the price you are asking for it, but I will refuse to buy it, in order to force you to lower the price." If he tries that, I will sell it to someone else instead. It is also appropriate in the monopoly situation I have been discussing in this chapter, where there is one seller and many buyers--although selling my speeches, with one seller and a few buyers, approaches the case of bilateral monopoly.
But the assumption that we can ignore bargaining, strategic behavior, and the like is inappropriate in all of the hard cases. If there are several sellers and many buyers, everything a seller wants to know about the buyers' behavior is summed up in the demand curve, but a seller cannot use a supply curve to describe the behavior of the other sellers, since they do not have supply curves. Each has an incentive to try to persuade the others to keep their production down, in order that he can sell lots of output at a high price; each has an incentive to threaten that if the other producers expand their output, he will expand his. In the case of bilateral monopoly, the seller has an incentive to try to persuade the buyer to pay a high price by threatening not to sell at a low one, even if selling at the low price is better than not selling at all. For similar reasons, bargaining, threats, and the like are important elements in the other situations that do not consist of many people on one side and either one or many on the other.
As you will see in the next chapter, analyzing strategic bargaining is a hard problem. It is a subset of the more general problem of solving n-person games. The Theory of Games and Economic Behavior by Von Neumann and Morgenstern was an attempt to solve the general problem; it is a great book but an unsuccessful attempt. Economists since have spent a good deal of effort trying to understand such situations, with rather limited success.
In addition to strategic behavior, this chapter has also ignored two other questions often associated with monopoly--is it a bad thing and if so what should we do about it? We take up those issues in Chapter 16, where we discuss why and under what circumstances monopolies produce undesirable outcomes, and the problems associated with trying to use government regulation to improve things.
It is interesting to apply some of the ideas of this chapter to the problem faced by Disneyland in setting its pricing policies. Over the years, it has used various combinations of an entry fee plus per-ride charges. When I was last there, the per-ride charges were zero--the admission ticket provided unlimited rides. A few years earlier, when I was a visiting professor at the University of California at Irvine, the hospitality package that I received from the housing office included a card that permitted me to buy an unlimited ride ticket. I do not believe such cards were being sold to the general public, although they must have been very widely available.
How should Disney decide what combination of entry fee and per-ride ticket price to charge? To begin with, assume that all customers (and all rides) are identical. Figure 10-12 shows one customer's demand for rides. The horizontal axis shows the number of rides he buys as a function of the price he must pay for each ride.
Suppose Disneyland requires a ticket, costing $1, for each ride. The customer will choose to go on 5 rides, paying Disneyland $5. At a price of $0.40, he would choose 8 rides and pay $3.20. At a price of $1.60, he would choose 2 rides and pay $3.20. At a price of $2, he would choose zero rides and pay nothing. What price should Disney charge?
The problem of choosing a ticket price appears to be the same as the problem of the price searcher trying to pick a price and quantity, which was analyzed in Part 1 of this chapter. If so, we know the solution; choose price so as to sell that number of rides for which marginal revenue is equal to marginal cost. If Disneyland's marginal cost is zero (it costs the same amount to run a ride whether or not anyone is on it), Disney should choose the price at which marginal revenue is zero and total revenue is at its maximum--$1/ride in this example.
That is the wrong answer. Disneyland need not limit itself to charging a price for the rides; it can and does also charge a price to come into the park. The more expensive the rides are, the lower the price that people will be willing to pay to enter. What Disney wants to maximize is revenue from entry tickets plus revenue from ride tickets minus costs; it cannot do so by simply setting the price of the ride ticket so as to maximize revenue from ride tickets.
Demand for rides at Disneyland--the
profit-maximizing price for a single-price monopoly. If the price
for a ride is $1, which maximizes revenue from the rides, the
consumer surplus, which is the amount that can be charged as an
admission price, is area A.
To figure out what combination of prices Disneyland should charge, we need to know exactly how the price people will pay for admission is affected by the price they are charged for the rides. Fortunately, we do. Area A on Figure 10-12 is the consumer surplus received by a consumer who is free to buy as many rides as he wishes at $1/ride. Since his consumer surplus is defined as the value to him of being able to buy rides at that price, it is also the maximum that he will pay for the right to do so--which he gets by entering Disneyland. Area A is the highest entry fee Disneyland can charge if it charges $1 for each ride; at any higher fee, customers will stop coming.
Area B on the figure is the number of rides the customer takes times the price of each ride ticket. So area B is the total revenue (from that customer) from ride tickets. Area A plus area B is Disney's total revenue from that customer--entry fee plus ride tickets. As you can easily see, the area is maximized if the ride price is zero, as shown in Figure 10-13a; the rides are free and all the money is made on the entry fee.
I have assumed that the cost to Disney of having one more person go on the ride is zero. Suppose that is not true; suppose it costs $0.20 more electricity to operate the ride with someone on it than with an empty seat. Figure 10-13b shows that situation, with price per ride set at $1. Area A is again consumer surplus (and maximum entry fee), but area B is now revenue from ride tickets minus the cost of those rides. Each ride the customer takes provides an extra $1 of income and an extra $0.20 of cost, for a net gain of $0.80. You should be able to satisfy yourself that the area A + B is now maximized by setting the price equal to $0.20 per ride--the marginal cost. The proof is the same one we have already seen twice--once in Chapter 4 for popcorn and once in this chapter for cookies.
There are at least two important complications we would have to add if we wanted to decide what the real Disneyland should do. One is that customers are not all identical; the admission price that one customer is more than willing to pay may be high enough to drive another customer away. If, on average, the customers who are willing to pay a high admission price are also the ones who go on a lot of rides, then a high price for rides is an indirect way of charging a high total price (rides plus admission) to those who are willing to pay it; this greatly complicates the problem of choosing an optimum ticket price.
The profit-maximizing per-ride price with
two-part pricing. At a price of zero, the sum of admission price
(A) and revenue from rides (B = 0 on Figure 10-13a) is maximized. If
MC = 0 for the ride, as shown on Figure 10-13a, this is the
profit-maximizing arrangement; if MC = .20, the profit-maximizing
price is $0.20/ride, as shown on Figure 10-13b.
The second important complication is that some rides may be used to capacity. In this case, my decision to go on one more ride imposes a cost--even if it takes no more electricity to run the ride full than empty. Since the ride is already full, the cost of my going on it is that someone else does not. My decision to take the ride lengthens the line of people waiting for it, imposing costs on everyone else in the line and persuading someone else to take one fewer ride.
This appears to be a cost imposed on the customers, not on the park; why should Disney care how long the customers stand in line? The answer is that how long they have to stand in line to go on a ride is one of the things affecting how much they value visiting Disneyland, hence how much they will pay for the admission ticket. By going on one more ride, you impose a cost directly on the other customers and indirectly on Disney; Disney should take that cost into account in deciding what price to charge for the ride. It turns out that (assuming all customers are identical) the optimal price is the one that just reduces the line to zero. You may find it easier to figure out why that is true after you finish Chapter 17.
In the discussion of popcorn at the end of Chapter 4, I showed that if customers are identical, theaters should sell popcorn at cost. One explanation of what we observe is that they do--that the high price of popcorn (and candy and soda) reflects high costs. Since the theater is selling food for only 20 minutes or so every two hours, perhaps its operating costs are much higher than those of other sellers.
In this chapter's discussion of discriminatory pricing, I suggested an alternative explanation, based on the fact that customers are not identical. If popcorn is expensive, the poor student who is just barely willing to pay $5 to see the movie will probably either do without or smuggle in his own, while the affluent student (or the one trying to impress a new date) will be willing both to pay a high price and to buy a lot of popcorn. The combination of cheap tickets and expensive popcorn is a way of keeping the business of the poor student while making as much as possible out of the rich one.
How could one find out which explanation is right? Discriminatory pricing is only possible if the seller has a considerable degree of monopoly; in a competitive industry, if you try to charge a higher price to richer customers, some other firm will undercut you. In a small town, there may be only one movie theater; even if there are several, it is unlikely that more than one is showing a particular movie at a particular time. Each theater is then a monopoly (with regard to its particular movie) and can engage in discriminatory pricing by, among other things, charging above-cost prices for food. In a large city, the customers can choose among many theaters, several of which may be showing the same film. If the discriminatory pricing explanation is correct, we would expect the difference between the price of popcorn or candy in a movie theater and its price elsewhere to be larger in small towns than in big cities. If, on the other hand, the difference reflects a difference in cost, we would probably expect the opposite result, since both labor and real estate--the two things that contribute to the high cost of a food concession in a theater that can only sell ten percent of the time--are generally more expensive in cities.
Figure 10-14a shows how price elasticity varies with quantity along a straight line demand curve. The figure has two vertical axes; the one on the left shows price, the one on the right elasticity. The slope of a straight line is the same everywhere (-1/2 for the demand curve shown on the figure) so dQ/dP = 1/(dP/dQ) = 1/(-1/2) = -2. Elasticity equals -(P/Q)dQ/dP; P/Q varies along the line. It is equal to infinity at the left end of D, where P = 10 and Q = 0; it is equal to zero at the right end, where Q = 20 and P = 0. Along the curve, elasticity varies as shown in Figure 10-14a. Points A, B, and C have been marked to allow you to check that the curve correctly shows the elasticity at those points.
Calculating the elasticity of a demand
curve. Each diagram shows demand and elasticity. Elasticity is
calculated at three points on Figure 10-14a and two points on Figure
10-14b.
Figure 10-14b shows the same information for a
demand curve that is not a straight line. Both dP/dQ--the slope--and
P/Q vary along the line. This time I have marked two points--a and
b--so that you can check my calculations. In each case, the
slope--dP/dQ--is calculated by taking the slope of a line tangent to
the curve at that point. Table 10-1 shows the calculations for
Figures 10-14a and 10-14b. ![]() P
and
P
and ![]() Q are the
vertical and horizontal intercepts of the tangent; their ratio is its
slope, which is equal to dP/dQ.
Q are the
vertical and horizontal intercepts of the tangent; their ratio is its
slope, which is equal to dP/dQ.
|
Point |
|
|
|
|
|
|
|
A |
|
|
|
|
-2 |
|
|
B |
|
|
|
|
-2 |
|
|
C |
|
|
|
|
-2 |
|
|
a |
|
|
|
|
-2.25 |
|
|
b |
|
|
|
|
-1.3 |
|
Figure 10-15 shows a simpler way of calculating price elasticity. The triangles GEC, HFE, and OFC are all similar. From the similarity of HFE and OFC, we have:
EF/EH = CF/CO.
Hence
EF = EH(CF/CO). (Equation 1)
From the similarity of GEC and OFC, we have:
CE/GE = CF/OF.
Hence
CE = GE(CF/OF) (Equation 2)
Dividing Equation 1 by Equation 2, we have:
EF/CE = (EH/GE)(OF/CO). (Equation 3)
But, as you can see from the figure, EH = P, GE = Q, and CO/OF is minus the slope of the line CF. The slope of CF is equal to the slope of the demand curve at the point E--which is dP/dQ. So OF/CO is -dQ/dP, and Equation 3 becomes:
EF/CE = (P/Q)(-dQ/dP) = elasticity of demand curve D at point E.
So one can calculate the elasticity of a demand curve by simply drawing the tangent and taking the ratio between EF (the distance from the point of tangency to the intersection with the quantity axis) and CE (the distance from the point of tangency to the intersection with the price axis). This gives us a simpler way of calculating the elasticity of a demand curve than the one shown on Table 10-1.
A simpler way of calculating elasticity.
The elasticity of the curve at point E is EF/CE.
Economies of scale are ways in which large firms can produce more cheaply than small ones; diseconomies of scale are the opposite. One important source of economies of scale is mass production; a firm that produces a million widgets per year can set up assembly lines, buy special widget-making machinery, and so forth. Another source may be economies of scale in administration; a large firm can afford to take advantage of specialization by having one executive deal with advertising and another with personnel. Economies of scale are usually important only up to some maximum size; that is why a large firm, such as GM or U.S. Steel, does not consist of one gigantic factory, as it would if such a factory could produce at a substantially lower cost than several large factories.
An important source of diseconomies of scale, as mentioned earlier, is the problem of coordinating a large firm. The fundamental organizational problem of a firm is the conflict between the interests of the employees and the interests of the owners. The owners want to maximize profits. The employees, while they have no objection to profits, would prefer to take more leisure, work less hard, or benefit themselves in other ways, even if the result is less profit for the owners. This problem is "solved" by supervisors who watch the employees, give raises to those who work hard, and fire those who do not. The supervisors are themselves employees and must themselves be monitored by a higher level of supervisors. Since such monitoring is neither costless nor perfectly effective, every additional layer increases costs and reduces performance. The more layers there are, the more the employees find themselves pursuing, not the interest of the firm, but what they think the person above them thinks the person above him thinks is the interest of the firm. Seen from this standpoint, the ideal arrangement is the one-person firm; if its sole employee chooses to slack off, he, being also the owner of the firm, pays the cost in reduced profits.
When I was choosing a publisher for this book, I had offers from two firms, one substantially larger and more prestigious than the other. I ended up choosing the smaller and less prestigious firm, in large part because in dealing with it I felt as though I was conversing with human beings--rather than being quoted to from a manual entitled How to Deal With Aspiring Authors. One reason for the difference may well have been that the people I dealt with at the smaller firm were a couple of layers closer to the top of their organization than were their opposite numbers at the larger firm.
If there were only diseconomies of scale, we would expect to see an economy of one-person firms, cooperating by trading goods and services with each other. Firms consisting of one person, one family, or a small number of individuals are common (writers, doctors, owners of small grocery stores), but so are much larger firms. It appears that diseconomies of scale are often balanced by economies of scale.
Consider an industry in which economies and diseconomies balance each other over a considerable range of production, giving the firm a cost function like that of Figure 10-16. Average cost is roughly constant over a large range of firm sizes, including a firm large enough to produce all of the output demanded at a price equal to average cost. It is widely believed that this is a common situation and one likely to lead to an artificial monopoly; the usual example is the Standard Oil Trust under John D. Rockefeller.
The argument goes as follows: I am Rockefeller and have somehow gotten control of 90 percent of the petroleum industry. My firm, Standard Oil, has immense revenues, from which it accumulates great wealth; its resources are far larger than the resources of any smaller oil company or even all of them put together. As long as other firms exist and compete with me, I can earn only the normal return on my capital and labor--economic profit equals zero. Any attempt to push up prices will cause my competitors to increase their production and may also draw additional firms into the industry.
A cost curve for an industry in which large and
small firms have about the same average cost.
I therefore decide to drive out my competitors by cutting prices to below average cost. Both I and my competitors lose money; since I have more money to lose, they go under first. I now raise prices to a monopoly level, calculated as if I were a natural monopoly (marginal cost equals marginal revenue). If any new firm considers entering the market to take advantage of the high prices, I point out what happened to my previous competitors and threaten to repeat the performance if necessary.
This argument is an example of the careless use of verbal analysis. "Both I and my competitors are losing money . . ." sounds very much as though we are losing the same amount of money. We are not. If I am selling 90 percent of all petroleum, a particular competitor is selling 1 percent, and we both sell at the same price and have the same average cost, I lose $90 for every $1 he loses.
My situation is worse than that. By cutting prices, I have caused the quantity demanded to increase; if I want to keep the price down, I must increase my production--and losses--accordingly. So I must actually lose (say) $95 for every $1 my competitor loses. Worse still, my competitor, who is not trying to hold down the price, may be able to reduce his losses and increase mine by reducing his production, forcing me to sell still more oil at less than production cost, and so lose still more money. He may even be able to close down temporarily and wait until I tire of throwing my money away and permit the price to go back up. Even if he has some costs that he cannot escape without going permanently out of business, he may be able to reduce his total losses by temporarily closing his older refineries, running some plants half time, and failing to replace employees who move or retire. If so, for every $95 or $100 I lose, he loses (say) $0.50.
But although I am bigger and richer than he is, I am not infinitely bigger and richer; I am 90 times as big and presumably about 90 times as rich. I am losing money more than 90 times as fast as he is; if I keep trying to drive him out by selling below cost, it is I, not he, who will go bankrupt first. Despite the widespread belief that Rockefeller maintained his position by selling oil below cost in order to drive competitors out of business (predatory pricing), a careful study of the record found no solid evidence that he had ever done so.
In one case, a Standard Oil official threatened to cut prices if a smaller firm, Cornplanter Oil, did not stop expanding and cutting into Standard's business. Here is the reply Cornplanter's manager gave, according to his own testimony:
Well, I says, "Mr. Moffett, I am very glad you put it that way, because if it is up to you the only way you can get it (the business) is to cut the market (reduce prices), and if you cut the market I will cut you for 200 miles around, and I will make you sell the stuff," and I says, "I don't want a bigger picnic than that; sell it if you want to" and I bid him good day and left. That was the end of that.
--quoted in John S. McGee, "Predatory Price Cutting: The Standard Oil (NJ) Case," Journal of Law and Economics, Vol. 2 (October, 1958), p.137.
In addition to predatory pricing, a variety of other tactics have been suggested for a firm trying to get and maintain an artificial monopoly. One is for the firm to buy out all of its competitors; it has been argued that this, rather than predatory pricing, is how Rockefeller maintained his position. The problem is that if every time someone builds a new refinery, Rockefeller has to buy him out, starting refineries becomes a very profitable business, and Rockefeller ends up with more refineries than he has any use for.
It is hard to prove that none of these tactics can ever work. If, for instance, Rockefeller can convince potential competitors that he is willing to lose an almost unlimited amount of money keeping them out, it is possible that no one will ever call his bluff--in which case it will cost him nothing. One can only say that the advantage in such a game seems to lie with the small firm, not the large, and that the bulk of the economic and historical evidence suggests that the artificial monopoly is mostly or entirely mythical.
One consequence of such myths may be to encourage monopoly. Selling at below cost is a poor way of driving your competitors out of business but may be a good way for a new firm to persuade customers to try its products. Under present antitrust law, a firm that does so risks being accused by its competitors of unfair competition and forced to raise its price. Laws that make life hard for new firms--or old firms entering new markets--reduce competition and encourage monopoly, even if they are called antitrust laws.
1. Economics is a competitive industry; my decision to become an economist or to teach one more course will not much affect the salary of economists. Economists as a group face a downward-sloping demand curve; the more there are, the less they can expect to get for their services. But each indidivdual economist faces an almost perfectly horizontal demand curve; his decision to teach more courses, write more books, do more consulting, or whatever will have a very small effect on the price he receives for doing so.
The argument does not apply to everything an economist does. This book, for example, may increase (or decrease!) your interest in becoming an economist; your decision to become an economist may affect the salary received by other economists--including me. How should that possibility affect my decision of how to write the book? If the book makes economics seem an attractive and interesting profession, what might you conjecture about how many copies I expect to sell?
2. Figure 10-17 shows two demand curves; draw the corresponding marginal revenue curves.
Demand Curves for Problem 2.
3. One can draw two different demand curves D1 and D2 such that a single-price monopoly would charge the same price whether faced by D1 or D2, but produce different quantities. One can also draw two curves D3 and D4 that result in the same quantity but different prices. Assuming that the producer has the MC curve of Figure 10-3a, draw demand curves D1-D4 .
4. Suppose a single-price monopoly has no production cost. What can you say about the elasticity of demand at the profit-maximizing quantity? Can you give an example of a monopoly with no production cost? With marginal cost equal to zero? If so, do.
5. Suppose a monopoly has MC > 0. What can you say about the elasticity of demand at the profit-maximizing quantity? Prove your result.
6. Suppose that some change in technology or input prices alters the fixed cost of a monopoly, while leaving the marginal cost curve unaffected. What is the effect on output and price? Explain.
7. Quercus, Inc. has been accused of violating the antitrust laws by charging a monopoly price for acorns. The firm's lawyer argues as follows: "While it is true that we produce most of the world's acorns, it has been shown by independent studies that the demand curve for acorns is elastic. If we tried to take advantage of our position by raising the price, we would only hurt ourselves by losing sales."
The lawyer for the antitrust division of the justice department replies: "I agree that, at the present price of acorns, the demand curve is elastic. That is evidence not that you are innocent but that you are guilty." Explain. Which lawyer is correct? Remember that evidence is not the same as proof; the question is only whether the observed elasticity of demand is evidence for or against the firm's guilt.
8. When I asked a realtor to find a house for me to buy, one of her first questions was, "How much do you want to spend?" This seems a rather odd question, since how much I want to spend, on houses or anything else, depends on what I can get for the money; even if I can buy a $200,000 house ($300,000 if enough of you buy this book), I might rather spend $100,000 if for that price I can get most of what I want. Why do you think the realtor puts the question this way? (Hint: Realtors are paid on commission; in most cities, they receive a fixed percentage of the value of the houses they sell.)
9. How should I answer the realtor in Problem 8? Should I tell her the maximum I am willing to spend for a house?
10. Figures 10-18a, 10-18b, and 10-18c show demand curves, marginal cost curves, and average cost curves for three single-price monopoly firms. In each case, how much should the firm produce and at what price should it sell in order to maximize its profit?
Demand and cost curves for Problems 10 and
11.
11. Suppose the firms in Problem 10 can engage in discriminatory pricing. Under what circumstances can they do so perfectly by using a two-part price? Assuming that they can do so, what should the two parts be for each firm--how large a per-unit charge and how large an admission charge? Assume that each firm has 100 customers.
12. Figures 10-19a and 10-19b show demand curves, marginal cost curves, and average cost curves for two monopolies. In the first case, there are 10 customers with demand curve DA and 10 with DB; in the second case, there are 10 type A and 5 type B customers. Note that average cost is shown as a function of total quantity produced, while each of the demand curves relates price to the quantity bought by a single customer.
a. In each case, draw the total demand curve and find the profit-maximizing price, assuming the firm is a single-price monopoly.
b. In each case, find the optimal two-part price (per-unit charge plus membership fee for the right to buy any units at all) assuming the per-unit fee must equal marginal cost.
c. In each case, find some two-part price that yields a higher profit than you got in part (b).
d. Is any general principle suggested by your answers to (c) ? If so, prove it if possible. (This is a hard problem.)
Demand and cost curves for Problem 12.
Cost curves for Problem 13.
The Supply curve for tractor tires for Problems
14 and 15, the MRP curve for Problem 14 only, and The demand curve
for tractors in Problem 16.
13. Figure 10-20 shows the cost curves for one firm in an industry. Can you tell whether the firm is or is not a natural monopoly? If not, what additional information do you need?
14. Figure 10-21a shows the supply curve for size 18 tractor tires. SuperOx, a tractor company, is the only purchaser of such tires. MRP is the marginal revenue product of such tires for SuperOx.
a. Draw the marginal expenditure curve for buying tires.
b. How many tires should SuperOx buy?
15. The supply curve for size 18 tires is the same as in the previous problem. SuperOx sells tractors on a competitive market at $20,000 apiece. Inputs are used in fixed proportions; each tractor requires exactly four tires, plus a bundle of other inputs which SuperOx purchases on a competitive market for $19,000.
a. Draw SuperOx's MRP curve (hint: It is not equal to MRP on Figure 10-21a).
b. How many tires should SuperOx buy?
16. The situation is the same as in the previous question, except that SuperOx is the only seller of tractors; the demand curve for tractors is shown on Figure 10-21b.
a. Draw SuperOx's MRP curve.
b. How many tires should SuperOx buy?
17. Give a brief verbal explanation of how you would analyse the buying and selling decisions of a firm that was both a monopoly and a monopsony.
18. Figure 10-22 shows a demand curve; graph the elasticity as was done on Figures 10-14a and 10-14b. You may use whichever method of calculating it you prefer.
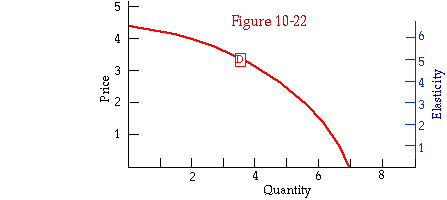
Demand curve for Problem 18.
Students interested in a detailed and original analysis of monopoly and price discrimination may want to look at the classic discussion of the subject in A. C. Pigou, The Economics of Welfare (London: Macmillan, 1932), especially Chapters XIV-XVII. A more modern source would be George Stigler, The Organization of Industry (Chicago: University of Chicago Press, 1968).
I am not the first economist to think of applying economic theory to the Magic Kingdom. You may wish to read Walter Oi, "A Disneyland Dilemma: Two-Part Tariffs for a Mickey Mouse Monopoly," Quarterly Journal of Economics, Vol. 85 (February, 1971), pp. 77-96.