Figure 11-1
"There are two kinds of people in the world: Johnny Von Neumann and the rest of us." Attributed to Eugene Wigner, a Nobel Prize winning physicist.
An economy is an interdependent system. In the process of solving it we have deliberately pushed that interdependency into the background. The individual, both as consumer and producer, is a small part of the market and can therefore take everyone else's behavior as given; he does not have to worry about how what he does will affect what they do. The rest of the world consists for him of a set of prices--prices at which he can sell what he produces and buy what he wants.
The monopolist of Chapter 10 is big enough to affect the entire market, but he is dealing with a multitude of individual consumers. Each consumer knows that what he does will not affect the monopolist's behavior. Each consumer therefore reacts passively to the monopolist, buying the quantity that maximizes the consumer's welfare at the price the monopolist decides to charge. From the standpoint of the monopolist, the customer is not a person at all; he is simply a demand curve.
Our analysis has thus eliminated an important feature of human interaction and of many markets--bargaining, threats, bluffs, the whole gamut of strategic behavior. That is one of the reasons why most of price theory seems, to many students, such a bloodless abstraction. We are used to seeing human society as a clash of wills, whether in the boardroom, on the battlefield, or in our favorite soap opera. Economics presents it instead in terms of solitary individuals, or at the most small teams of producers, each calmly maximizing against an essentially nonhuman environment, an opportunity set rather than a population of self-willed human beings.
There is a reason for doing economics this way. The analysis of strategic behavior is an extraordinarily difficult problem. John Von Neumann, arguably one of the smartest men of this century, created a whole new branch of mathematics in the process of failing to solve it. The work of his successors, while often ingenious and mathematically sophisticated, has not brought us much closer to being able to say what people will or should do in such situations. Seen from one side, what is striking about price theory is the unrealistic picture it presents of the world around us. Seen from the other, one of its most impressive accomplishments is to explain a considerable part of what is going on in real markets while avoiding, with considerable ingenuity, any situation involving strategic behavior. When it fails to do so, as in the analysis of oligopoly or bilateral monopoly, it rapidly degenerates from a coherent theory to a set of educated guesses.
What Von Neumann created, and what this chapter attempts to explain, is game theory. I start, in Part 1, with an informal description of a number of games, designed to give you a feel for the problems of strategic behavior. Part 2 contains a more formal analysis, discussing various senses in which one might "solve" a game and applying the solution concepts to a number of interesting games. Parts 3 and 4 show how one can attempt, with limited success, to apply the ideas of game theory to specific economic problems.
"Scissors, Paper, Stone" is a simple game played by children. At the count of three, the two players simultaneously put out their hands in one of three positions: a clenched fist for stone, an open hand for paper, two fingers out for scissors. The winner is determined by a simple rule: scissors cut paper, paper covers stone, stone breaks scissors.
The game may be represented by a 3x3 payoff matrix, as shown in Figure 11-1. Rows represent strategies for player 1, columns represent strategies for Player 2. Each cell in the matrix is the intersection of a row and a column, showing what happens if the players choose those two strategies; the first number in the cell is the payoff to Player 1, the second the payoff to Player 2. It is convenient to think of all payoffs as representing sums of money, and to assume that the players are simply trying to maximize their expected return--the average amount they win--although, as you will see, game theory can be and is used to analyze games with other sorts of payoffs.
Figure 11-1
The payoff matrix for Scissors, Paper, Stone.
The top left cell shows what happens if both players choose scissors; neither wins, so the payoff is zero to each. The next cell down shows what happens if Player 1 chooses paper and Player 2 chooses scissors. Scissors cuts paper, so Player 2 wins and Player 1 loses, represented by a gain of one for Player 2 and a loss of one for Player 1.
I have started with this game for two reasons. The first is that, because each player makes one move and the moves are revealed simultaneously, it is easily represented by a matrix such as Figure 11-1, with one player choosing a row, the other choosing a column, and the outcome determined by their intersection. We will see later that this turns out to be a way in which any two-person game can be represented, even a complicated one such as chess.
The second reason is that although this is a simple game, it is far from clear what its solution is--or even what it means to solve it. After your paper has been cut by your friend's scissors, it is easy enough to say that you should have chosen stone, but that provides no guide for the next move. Some quite complicated games have a winning strategy for one of the players. But there is no such strategy for Scissors, Paper, Stone. Whatever you choose is right or wrong only in relation to what the other player chooses.
While it may be hard to say what the correct strategy is, one can say with some confidence that a player who always chooses stone is making a mistake; he will soon find that his stone is always covered. One feature of a successful strategy is unpredictability. That insight suggests the possibility of a deliberately randomized strategy.
Suppose I choose my strategy by rolling a die, making sure the other player is not watching. If it comes up 1 or 2, I play scissors; 3 or 4, paper; 5 or 6, stone. Whatever strategy the other player follows (other than peeking at the die or reading my mind), I will on average win one third of the games, lose one third of the games, and draw one third of the games.
Can there be a strategy that consistently does better? Not against an intelligent opponent. The game is a symmetrical one; the randomized strategy is available to him as well as to me. If he follows it then, whatever I do, he will on average break even, and so will I.
One important feature of Scissors, Paper, Stone is that it is a zero-sum game; whatever one player wins the other player loses. While there may be strategy of a sort in figuring out what the other player is going to do, much of what we associate with strategic behavior is irrelevant. There is no point in threatening to play stone if the opponent does not agree to play scissors; the opponent will refuse, play paper, and cover your stone.
Consider next a game discussed in an earlier chapter--bilateral monopoly. The rules are simple. You and I have a dollar to divide between us, provided that we can agree on a division. If we cannot agree, the dollar vanishes.
This game is called bilateral monopoly because it corresponds to a market with one buyer and one seller. I have the world's only apple and you are the only person in the world not allergic to apples. The apple is worth nothing to me and one dollar to you. If I sell it to you for a dollar, I am better off by a dollar and you, having paid exactly what the apple is worth, are just as well off as if you had not bought it. If I give it to you, I gain nothing and you gain a dollar. Any price between one and zero represents some division of the dollar gain between us. If we cannot agree on a price I keep the apple and the potential gain from the trade is lost.
Bilateral monopoly nicely encapsulates the combination of common interest and conflict of interest, cooperation and competition, typical of many human interactions. The players have a common interest in reaching agreement but a conflict over what the terms of the agreement will be. The United States and the Soviet Union have a common interest in preserving peace but a conflict over how favorable the terms of that peace will be to each side. Husband and wife have a common interest in preserving a happy and harmonious marriage but innumerable conflicts over how their limited resources are to be spent on things that each values. Members of a cartel have a common interest in keeping output down and prices up but a conflict over which firm gets how much of the resulting monopoly profit.
Bilateral monopoly is not a zero-sum game. If we reach agreement, our gains sum to $1; if we fail to reach agreement, they sum to zero. That makes it fundamentally different from Scissors, Paper, Stone; it permits threats, bargains, negotiation, bluff.
I decide to get 90 cents of the dollar gain. I inform you that I will refuse to accept any less favorable terms; you may choose between 10 cents and nothing. If you believe me, you give in. If you call my bluff and insist that you will only give me 40 cents, I in turn, if I believe you, have the choice of 40 cents or nothing. Each player is trying to get a better outcome for himself by threatening to force an outcome that is worse for both.
One way to win such a game is to find some way to commit oneself, to make it impossible to back down. A child with good strategic instincts might announce "I promise not to let you have more than 20 cents of the dollar, cross my heart and hope to die." If the second player believes that the oath is binding--that the first player will not back down because no share of the dollar is worth the shame of breaking the oath--the strategy works. The second player goes home with 20 cents and a resolution that next time he will get his promise out first.
The strategy of commitment is not limited to children. Its most dramatic embodiment is the doomsday machine, an idea dreamed up by Hermann Kahn and later dramatized in the movie Doctor Strangelove.
Suppose the United States decides to end all worries about Soviet aggression once and for all. It does so by building a hundred cobalt bombs, burying them in the Rocky Mountains, and attaching a fancy geiger counter. If they go off, the cobalt bombs produce enough fallout to eliminate all human life anywhere on earth. The geiger counter is the trigger, set to explode the bombs if it senses the radiation from a Soviet attack.
We can now dismantle all other defenses against nuclear attack; we have the ultimate deterrent. In an improved version, dubbed by Kahn the Doomsday-in-a-hurry Machine, the triggering device is somehow equipped to detect a wide range of activities and respond accordingly; it could be programmed, for instance, to blow up the world if the Soviets invade West Berlin, or West Germany, or anywhere at all--thus saving us the cost of a conventional as well as a nuclear defense.
While a doomsday machine is an elegant idea, it has certain problems. In Doctor Strangelove, it is the Russians who build one. They decide to save the announcement for the premier's birthday. Unfortunately, while they are waiting, a lunatic American air force officer launches a nuclear strike against the Soviet Union.
The doomsday machine is not entirely imaginary. Consider the situation immediately after the United States detects the beginning of an all-out nuclear strike by the Soviet Union. Assume that, as is currently the case, we have no defenses, merely the ability to retaliate. The threat of retaliation may prevent an attack, but if the attack comes anyway retaliation will not protect anyone. It may even, by increasing fallout, climactic effects, and the like, kill some Americans--as well as millions of Russians and a considerable number of neutrals who have the misfortune to be downwind of targets.
Retaliation in such a situation is irrational. Nonetheless, it would probably occur. The people controlling the relevant buttons--bomber pilots, air force officers in missile silos, nuclear submarine captains--have been trained to obey orders. They are particularly unlikely to disobey the order to retaliate against an enemy who has just killed, or is about to kill, most of their friends and family.
Our present system of defense by retaliation is a doomsday machine, with human beings rather than geiger counters as the trigger. So is theirs. So far both have worked, with the result that neither has been used. Kahn invented the idea of a doomsday machine not because he wanted the United States to build one but because both we and the Soviet Union already had.
Between "cross my heart and hope to die" and nuclear annihilation, there is a wide range of situations where threat and commitment play a key role. Even before the invention of nuclear weapons, warfare was often a losing game for both sides. A leader who could persuade the other side that he was nonetheless willing to play, whether because he was a madman, a fanatic, or merely an optimist, was in a strong bargaining position. They might call his bluff--but it might not be a bluff.
Another example was mentioned in the discussion of artificial monopoly in the previous chapter. If Rockefeller can somehow convince potential entrants to the refining business that if they build a refinery he will drive them out whatever the cost, he may be able to maintain a monopoly. If someone calls his bluff and he really has committed himself, he may have to spend his entire fortune trying, perhaps unsuccessfully, to carry out his threat.
There are many examples of the same logic on a smaller scale. Consider a barroom quarrel that starts with two customers arguing about baseball teams and ends with one dead and the other standing there with a knife in his hand and a dazed expression on his face. Seen from one standpoint, this is a clear example of irrational and therefore uneconomic behavior; the killer regrets what he has done as soon as he does it, so he obviously cannot have acted to maximize his own welfare. Seen from another standpoint, it is the working out of a rational commitment to irrational action--the equivalent, on a small scale, of a doomsday machine going off.
Suppose I am strong, fierce, and known to have a short temper with people who do not do what I want. I benefit from that reputation; people are careful not to do things that offend me. Actually beating someone up is expensive; he may fight back, and I may get arrested for assault. But if my reputation is bad enough, I may not have to beat anyone up.
To maintain that reputation, I train myself to be short-tempered. I tell myself, and others, that I am a real he-man, and he-men don't let other people push them around. I gradually expand my definition of "push me around" until it is equivalent to "don't do what I want."
We usually describe this as an aggressive personality, but it may make just as much sense to think of it as a deliberate strategy rationally adopted. Once the strategy is in place, I am no longer free to choose the optimal response in each situation; I have invested too much in my own self-image to be able to back down. In just the same way, the United States, having constructed a system of massive retaliation to deter attack, is not free to change its mind in the ten minutes between the detection of enemy missiles and the deadline for firing our own. Not backing down once deterrence has failed may be irrational, but putting yourself in a situation where you cannot back down is not.
Most of the time I get my own way; once in a while I have to pay for it. I have no monopoly on my strategy; there are other short-tempered people in the world. I get into a conversation in a bar. The other guy fails to show adequate deference to my opinions. I start pushing. He pushes back. When it is over, one of us is dead.
Two men are arrested for a robbery. If convicted, each will receive a jail sentence of two to five years; the actual length depends on what the prosecution recommends. Unfortunately for the District Attorney, he does not yet have enough evidence to get a conviction.
The DA puts the criminals in separate cells. He goes first to Joe. He tells him that if he confesses and Mike does not, the DA will drop the burglary charge and let Joe off with a slap on the wrist--three months for trespass. If Mike also confesses, the DA cannot drop the charge but he will ask the judge for leniency; Mike and Joe will get two years each.
If Joe refuses to confess, the DA will not feel so friendly. If Mike confesses, Joe will be convicted and the DA will ask for the maximum possible sentence. If neither confesses, the DA cannot convict them of the robbery, but he will press for a six-month sentence for trespass, resisting arrest, and vagrancy.
After explaining all of this to Joe, the DA goes to Mike's cell and gives the same speech, with names reversed. Figure 11-2 shows the matrix of outcomes facing Joe and Mike.
Joe reasons as follows:
If Mike confesses and I don't, I get five years; if I confess too, I get two years. If Mike is going to confess, I had better confess too.
If neither of us confesses, I go to jail for six months. That is a considerable improvement on what will happen if Mike squeals, but I can do better; if Mike stays silent and I confess, I only get three months. So if Mike is going to stay silent, I am better off confessing. In fact, whatever Mike does I am better off confessing.
Figure 11-2
The payoff matrix for prisoner's dilemma.
Joe calls for the guard and asks him to send for the DA. It takes a while; Mike has made the same calculation, reached the same conclusion, and is in the middle of dictating his confession.
This game has at least two interesting properties. The first is that it introduces a new solution concept. Both criminals confess because each calculates, correctly, that confession is better than silence whatever the other criminal does. We can see this on Figure 11-2 by noting that the column "Confess" has a higher payoff for Joe than the column "Say Nothing," whichever row Mike chooses. Similarly, the row "Confess" has a higher payoff for Mike than the row "Say Nothing," whichever column Joe chooses.
If one strategy leads to a better outcome than another whatever the other player does, the first strategy is said to dominate the second. If one strategy dominates all others, then the player is always better off using it; if both players have such dominant strategies, we have a solution to the game.
The second interesting thing is that both players have acted rationally and both are, as a result, worse off. By confessing, they each get two years; if they had kept their mouths shut, they each would have gotten six months. It seems odd that rationality, defined as making the choice that best achieves the individual's ends, results in both individuals being worse off.
The explanation is that Joe is only choosing his strategy, not Mike's. If Joe could choose between the lower right-hand cell of the matrix and the upper left-hand cell, he would choose the former; so would Mike. But those are not the choices they are offered. Joe is choosing a column, and the left-hand column dominates the right-hand column; it is better whichever row Mike chooses. Mike is choosing a row, and the top row dominates the bottom.
We have been here before. In Chapter 1, I pointed out that rationality is an assumption about individuals not about groups, and described a number of situations where rational behavior by the individuals in a group made all of them worse off. This is the same situation in its simplest form--a group of two. Prisoners confess for the same reason that armies run away and students take shortcuts across newly planted lawns.
To many of us, the result of prisoner's dilemma and similar games seems deeply counter-intuitive. Armies do not always run away, at least in part because generals have developed ways of changing the structure of rewards and punishments facing their soldiers. Burning your bridges behind you is one solution; shooting soldiers who run away in battle is another. Similarly, criminals go to considerable effort to raise the cost to their co-workers of squealing and lower the cost of going to jail for refusing to squeal.
But none of that refutes the logic of prisoner's dilemma; it merely means that real prisoners and real soldiers are sometimes playing other games. When the net payoffs to squealing, or running, do have the structure shown in Figure 11-2, the logic of the game is compelling. Prisoners confess and soldiers run.
One obvious response to the analysis of the prisoner's dilemma is that its result is correct, but only because the game is being played only once. Many real-world situations involve repeated plays. Mike and Joe will eventually get out of jail, resume their profession, and be caught again. Each knows that if he betrays his partner this time around, he can expect his partner to treat him similarly next time, so they both refuse to confess.
The argument is persuasive, but it is not clear if it is right. Suppose we abandon Joe and Mike, and consider instead two people who are going to play a game like the one represented by Figure 11-2 a hundred times. To make their doing so more plausible, we replace the jail sentences of Figure 11-2 with positive payoffs. If both players cooperate, they get $10 each. If each betrays the other, they get nothing. If one betrays and the other cooperates, the traitor gets $15 and the patsy loses $5.
A player who betrays his partner gains five dollars in the short run, but the gain is not likely to be worth the price. The victim will respond by betraying on the next turn, and perhaps several more. On net, it seems that both players are better off cooperating every turn.
There is a problem with this attractive solution. Consider the last turn of the game. Each player knows that whatever he does, the other will have no further opportunity to punish him. The last turn is therefore an ordinary prisoner's dilemma. Betraying dominates cooperating for both players, so both betray and each gets zero.
Each player can work through this logic for himself, so each knows that the other will betray him on the hundredth move. Knowing that, I know that I need not fear punishment for anything I do on the ninety-ninth move; whatever I do, you are in any case going to betray me on the next (and last) move. So I betray you on the ninety-ninth move--and you, having gone through the same calculation, betray me.
Since we know that we are both going to betray on the ninety-ninth move, there is now no punishment for betraying on the ninety-eighth move. Since we know we are going to betray on the ninety-eighth, there is no punishment for betraying on the ninety-seventh. The entire chain of moves unravels; if we are rational we betray each other on the first move and every move thereafter, ending up with nothing. If we had been irrational and cooperated, we would each have ended up with a thousand dollars.
If you find the result paradoxical, you have lots of company. Nonetheless, the argument is correct. It is only a minor relief to note that the analysis depends on the players knowing how many moves the game will last; if they are playing a finite but indefinite number of times, cooperation may be stable. We will return to this particularly irritating game at the end of Part 2 of this chapter.
So far, all of our games have had only two players. Consider the following very simple three-person game. There are three people--Anne, Bill, and Charles--and a hundred dollars. The money is to be divided by majority vote; any allocation that receives two votes wins.
Think of the play of the game as a long period of bargaining followed by a vote. In the bargaining, players suggest divisions and try to persuade at least one other player to go along. Each player is trying to maximize his own return--his share of the money.
Bill starts by proposing to Anne that they divide the money between them, $50 for each. That sounds to her like a good idea--until Charles proposes a division of $60 for Anne and $40 for himself. Charles makes the offer because $40 is better than nothing; $60 is better than $50, so Anne is happy to switch sides.
The bargaining is not ended. Bill, who is now out in the cold, suggests to Charles that he will be happy to renew his old proposal with a different partner; Charles will get $50, which is better than $40, and Bill will get $50, which is better than nothing.
The potential bargaining is endless. Any division anyone can suggest is dominated by some other division, and so on indefinitely. A division that gives something to everyone is dominated by an alternative with one player left out and his share divided between the other two. A division that does not give something to everyone is dominated by another in which the player who is left out allies with one of the previous winners and they split the share of the third player between them.
In Part 2, we will see how game theorists have tried to deal with such problems. For the moment, it is worth noting two concepts that we have introduced here and will use later. One concept is a division--what we will later call an imputation--an outcome of the game, defined by who ends up with what. The other is a new meaning for dominance: One division dominates another if enough people prefer it to make it happen.
The idea of game theory, as conceived by Von Neumann and presented in the book that he co-authored with economist Oskar Morgenstern, was to find a general solution to all games. That did not mean learning to play chess, or bridge, or poker, or oligopoly, perfectly. It meant figuring out how you would figure out how to play those games, or any others, perfectly. If one knew how to set up any game as an explicit mathematical problem, the details of the solution of each particular game could be left to someone else.
Seen from this standpoint, chess turns out to be a trivial game. The rules specify that if no pawn is moved and no piece taken for forty moves, the game is a draw. That means that the total number of moves, and thus the total number of possible chess games, is limited--very large but finite. To play chess perfectly, all you need do is list all possible games, note on each who wins, and then work backward from the last move, assuming at each step that if a player has a move that leads to an eventual win he will take it.
This is not a very practical solution to the problem of beating your best friend at chess. The number of possible games is much larger than the number of atoms in this galaxy, so finding enough paper to list them all would be difficult. But game theorists, with a few exceptions, are not interested in that sort of difficulty. Their objective is to figure out how the game would be solved; they are perfectly willing to give you an unlimited length of time to solve it in.
In analyzing games, we will start with two-person games. The first step in solving them will be to show how any two-person game can be represented in a reduced form analogous to Figure 11-1. The next step will be to show in what sense the reduced form of a two-person fixed-sum game can be solved. We will then go on to discuss a variety of different solution concepts for games with more than two players.
We normally think of a chess game as a series of separate decisions; I make a first move, you respond, I respond to that, and so forth. We can, however, describe the same game in terms of a single move by each side. The move consists of the choice of a strategy describing what the player will do in any situation. Thus one possible strategy might be to start by moving my king's pawn forward two squares, then if the opponent moves his king's pawn forward respond by . . . , if the opponent moves his queen's pawn instead respond by . . . , . . . The strategy would be a complete description of how I would respond to any sequence of moves I might observe my opponent making (and, in some games, to any sequence of random events, such as the fall of a die or what cards happen to be dealt).
Since a strategy determines everything you will do in every situation, playing the game--any game--simply consists of each side picking one strategy. The decisions are effectively simultaneous; although you may be able to observe your opponent's moves as they are made, you cannot see inside his head to observe how he has decided to play the game. Once the two strategies are chosen, everything is determined. One can imagine the two players writing down their strategies and then sitting back and watching as a machine executed them. White makes his first move, black makes his prechosen response, white makes his prechosen response to that, and so on until one side is mated or the game is declared a draw.
Seen in these terms, any two-person game can be represented by a payoff matrix like Figure 11-1, although it may require enormously more rows and columns. Each row represents a strategy that Player 1 could choose, each columnb represents a strategy that Player 2 could choose. The cell at the intersection shows the outcome of that particular pair of strategies. If the game contains random elements, the cell contains the expected outcome--the average payoff over many plays of the game. In game theory, this way of describing a game is called its reduced form.
This is not a very useful way of thinking about chess if you want to win chess games; there is little point wasting your time figuring out in advance how to respond to all the things your opponent might conceivably do. It is a useful way of thinking about chess, and poker, and craps, if you want to find some common way of describing all of them in order to figure out in what sense games have solutions and how, in principle, one could find them.
What is a solution for a two-person game? Von Neumann's answer is that a solution (for a zero-sum game) is a pair of strategies and a value for the game. Strategy S1 guarantees player 1 that she will get at least the value V, strategy S2 guarantees player 2 that he will lose at most V. V may be positive, negative, or zero; the definition makes no assumption about which player is in a stronger position.
Player 1 chooses S1 because it guarantees her V, and player 2, if he plays correctly (chooses S2) can make sure she does no better than that. Player 2 chooses S2 because it guarantees him -V, and player 1, if she plays correctly (chooses S1) can make sure he does no better than that.
Two obvious questions arise. First, is this really a solution; is it what a sufficiently smart player would choose to do? Second, if we accept this definition, do all two-person games have solutions?
The Von Neumann solution certainly does not cover everything a good player tries to do. It explicitly ignores what bridge players refer to as stealing candy from babies--following strategies that work badly against good opponents but exploit the mistakes of bad ones. But it is hard to see how one could eliminate that omission while constructing a better definition of a solution. There are, after all, many different opponents one might play and many different mistakes they might make; how do you define a "best" strategy against all of them? It seems reasonable to define a solution as the correct way to play against an opponent who is himself playing correctly.
Whether a solution exists for a game depends on what its reduced form looks like. Figure 11-3 shows the reduced form of a game that has a solution in this sense.
Figure 11-3
The payoff matrix for a game with a Von-Neumann
solution.
The central cell is the solution; it is the result of Anne choosing strategy II and Bill choosing strategy B. You can see that it is a solution by checking the alternatives. Given that Bill is choosing B, Anne is correct to choose II; anything else wins her zero instead of one. Given that Anne is choosing II, Bill is correct to choose B; anything else loses him two instead of one. The value of the game is -1. By choosing strategy B, Bill guarantees that he will not lose more than 1; by choosing strategy II Anne guarantees that she will win at least 1.
A strategy of this sort is sometimes called a minimax strategy; the solution is referred to as a saddle point. It is called a minimax because, seen from Bill's standpoint, he is minimizing the maximum amount he can lose; he acts as if he were assuming that, whatever he does, Anne will pick the right strategy against him. If he chose A, Anne could choose II, in which case he would lose 2; if he chose C, Anne could choose III, in which case he would lose 4. Precisely the same thing is true from Anne's standpoint; strategy II is her minimax as well. The Von Neumann solution has the interesting characteristic that each player acts as if the other one knew what he was going to do. One player does not in fact know what strategy the other is choosing, but he would do no better if he did.
Unfortunately, there is no reason to expect that all games will have saddle points. A simple counterexample is Scissors, Paper, Stone. If you look back at Figure 11-1, you will see that there is no cell with the characteristics of the solution shown on Figure 11-3. If, for example, Player 1 chooses scissors, then Player 2's best response is stone; but if Player 2 chooses stone, Scissors is Player 1's worst response; he should choose paper instead. The same is true for any cell. There is no saddle point.
Nonetheless, there is a Von Neumann solution, and we have already seen it. The trick is to allow players to choose not only pure strategies, such as A, B, C, or Scissors, Paper, Stone, but also mixed strategies. A mixed strategy is a probability mix of pure strategies--a 10% chance of A, a 40% chance of B, and a 50% chance of C, for instance. The solution to Scissors, Paper, Stone, as described in Part 1, is such a mixed strategy --an equal chance of following each of the three pure strategies. A player who follows that mixed strategy will lose, on average, zero, whatever his opponent does. A player whose opponent follows that strategy will win, on average, zero, whatever he does. So the Von Neumann solution is for each player to adopt that strategy. It is not only a solution but the only solution; if the player follows any one pure strategy (say stone) more frequently than the other two, his opponent can win more often than he loses by always picking the pure strategy (paper) that wins against that one.
We have now seen what a Von Neumann solution is and how a game that has no solution in terms of pure strategies may still have a mixed-strategy solution. Von Neumann's result is a good deal stronger than that. He proved that every two-person fixed-sum game has a solution, although it may require mixed strategies. He thus accomplished his objective for that class of games. He defined what a solution was, proved that one always existed, and in the process showed how, in principle, you would find it--provided, of course, that you had enough computing power and unlimited time. He also did his part to deal with at least the former proviso; one of the other things Von Neumann helped invent was cybernetics, the mathematical basis for modern computers.
If you look at Figures 11-1 and 11-3, you will note that both of the games are zero-sum. The numbers in each cell sum to zero; whatever one player wins the other loses. A zero-sum game is a special case of a fixed-sum game, one for which the total return to the two players, while not necessarily zero, is independent of what they do. As long as we limit ourselves to fixed-sum games, the interest of the two players is directly in conflict, since each can increase his winnings only by reducing the other player's.
This conflict is an important element in the Von Neumann solution. Bill chooses the strategy that minimizes his maximum because he knows that Anne, in choosing her strategy, is trying to maximize her gain--and her gain is his loss. The Von Neumann solution is not applicable to two-person variable-sum games such as bilateral monopoly or prisoner's dilemma, nor to many-person games.
For games with more than two players, the results of game theory are far less clear. Von Neumann himself proposed a definition of a solution, but not a very satisfactory one; it, and another solution concept growing out of Von Neumann's work, will be discussed in the optional section of this chapter. In this section, we will discuss another solution concept--a generalization of an idea developed by a French economist/mathematician early in the nineteenth century.
Nash Equilibrium. Consider an n-person game played not once but over and over, or continuously, for a long time. You, as one player, observe what the other players are doing and alter your play accordingly. You act on the assumption that what you do will not affect what they do, perhaps because you do not know how to take such effects into account, perhaps because you believe the effect of your play on the whole game is too small to matter.
You keep changing your play until no further change will make you better off. All the other players do the same. Equilibrium is finally reached when each player has chosen a strategy that is optimal for him, given the strategies that the other players are following. This solution to a many-player game is called a Nash equilibrium and is a generalization by John Nash of an idea invented by Antoine Cournot more than a hundred years earlier.
Consider, as a simple example, the game of driving, where choosing a strategy consists of deciding which side of the road to drive on. The United States population is in a Nash equilibrium; everyone drives on the right. The situation is stable, and would be stable even with no traffic police to enforce it. Since everyone else drives on the right, my driving on the left would impose very large costs on me (as well as others); so it is in my interest to drive on the right too. The same logic applies to everyone, so the situation is stable.
In England, everyone drives on the left. That too is a Nash equilibrium, for the same reason. It may well be an undesirable Nash equilibrium. Since in most other countries people drive on the right, cars have to be specially manufactured with steering wheels on the right side for the English market. Foreign tourists driving in England may automatically drift into the right-hand lane and discover their error only when they encounter an English driver face to face--and bumper to bumper. This is particularly likely, in my experience, when making a turn; there is an almost irresistible temptation to come out of it on what your instincts tell you is the correct side of the road.
If all English drivers switched to driving on the right, they might all be better off. But any English driver who tried to make the switch on his own initiative would be very much worse off. A Nash equilibrium is stable against individual action even when it leads to an undesirable outcome.
A Nash equilibrium may not be stable against joint action by several people; that is one of the problems with using it to define the solution to a many-person game. The Swedish switch to driving on the right is an extreme example; everyone changed his strategy at once. In some other games, a particular outcome is stable as long as everyone acts separately but becomes unstable as soon as any two people decide to act together. Consider the case of a prison guard with one bullet in his gun, facing a mob of convicts escaping from death row. Any one convict is better off surrendering; the small chance of a last-minute pardon or successful appeal is better than the certainty of being shot dead. Any two convicts are better off charging the guard.
A Nash equilibrium is not, in general, unique, as the case of driving shows; both everyone driving on the left and everyone driving on the right are equilibria. There is also another and more subtle sense in which a Nash equilibrium may not be unique. Part of its definition is that my strategy is optimal for me, given the strategies of the other players; I act as if what I do has no effect on what they do. But what this means depends on how we define a strategy. My action will in fact affect the other players; what response by them counts as continuing to follow the same strategy? As you will see in Part 4 of this chapter, different answers to that question correspond to different Nash equilibria for otherwise identical games.
While this is the first time we have discussed Nash equilibrium, it is not the first time we have used the idea. The grocery store and the freeway in Chapter 1 and the markets in Chapter 7, with price where supply crossed demand, were all in Nash equilibrium; each person was acting correctly, given what everyone else was doing
In each of these cases, it is interesting to ask how stable the equilibrium is. Would our conclusions be any different if we allowed two or three or ten people to act together, instead of assuming that each person acts separately? Does our result depend on just how we define a strategy? You may want to return to these questions after seeing how Nash equilibrium is used to analyze monopolistic competition in Part 3 of this chapter, and the behavior of oligopolies in Part 4.
In everything we have done so far, the players have been assumed to have an unlimited ability to calculate how to play the game--even to the extent of considering every possible chess game before making their first move. The reason for that assumption is not that it is realistic; obviously for most games it is not. The reason is that it is relatively straightforward to describe the perfect play of a game--whatever the game, the perfect strategy is the one that produces the best result.
It is much more difficult to create a theory of just how imperfect the decisions of a more realistic player with limited abilities will be. This is the same point made in Chapter 1, where I defended the assumption of rationality on the grounds that there is usually one right answer to a problem but a large number of wrong ones. As long as the individual has some tendency to choose the right one, we may be better off analyzing his behavior as if he always chose it than trying to guess which of the multitude of wrong decisions he will make.
There have been numerous attempts by economists and game theorists to get around this problem, to somehow incorporate within the theory the idea that players have only a limited amount of memory, intelligence, and time with which to solve a game. One of the most interesting attempts involves combining game theory with another set of ideas also descending, in large part, from John Von Neumann's fertile brain--the theory of computers. We cannot clearly define what kind of mistake an imperfect human will make, but we can clearly define what sort of strategies a particular computer can follow. If we replace the human with a computer, we can give precise meaning to the idea of limited rationality. In doing so, we may be able to resolve those puzzles of game theory that are created by the "simplifying assumption" of unlimited rationality.
Suppose we have a simple game--repeated prisoner's dilemma, for instance. The game is played by humans, but they must play through computers with specified abilities. Each computer has a limited number of possible states, corresponding to its limited amount of memory; you may think of a state as representing its memory of what has so far happened in the game. The computer bases its move on what has so far happened, so each state implies a particular move--cooperate or betray in the case of prisoner's dilemma.
The history of the game after any turn consists of the history before the turn plus what the opponent did on the turn, so the computer's state after a turn is determined by its state before and the opponent's move. Each player programs his computer by choosing the state it starts in, what move each state implies, and what new state results from each state plus each possible move the opponent could make. The players then sit back and watch the computers play.
One attractive feature of this approach is that it gives a precise meaning to the idea of bounded rationality; the intelligence of the computer is defined as the number of possible states it can be in. One can then prove theorems about how the solution to a particular game depends on the intelligence of the players.
Consider the game of repeated prisoner's dilemma with 100 plays. Suppose it is played by computers each of which has only 50 possible states. The state of the computer is all it knows about the past; with only 50 states the computer cannot distinguish the 100 different situations corresponding to "it is now the first move," "it is now the second move," ... "it is now the last move." Put in human terms, it is too stupid to count up to 100.
The cooperative solution to repeated prisoner's dilemma is unstable because it always pays to betray on the last play. Knowing that, it pays to betray on the next-to-last play, and so on back to the beginning. But you cannot adopt a strategy of betraying on the hundredth round if you cannot count up to 100. With sufficiently bounded rationality the cooperative solution is no longer unstable.
So far, I have discussed only theory. Games can also be analyzed by the experiment of watching people play them and seeing what happens; such work is done by both psychologists and economists.
Recently, a new and different experimental technique has appeared. A few years ago, a political scientist named Robert Axelrod conducted a prisoner's dilemma tournament. He invited all interested parties to submit strategies for repeated prisoner's dilemma; each strategy was to take the form of a computer program. He loaded all of the strategies into a computer and ran his tournament, with each program playing 200 rounds against each other program. When the tournament was over he summed the winnings of each program and reported the resulting score.
Sixteen programs were submitted, some of them quite complex. The winner, however, was very simple. It cooperated on the first round, betrayed in any round if the opponent had betrayed in the round before, and cooperated otherwise. Axelrod named it "tit-for-tat," since it punished betrayal by betraying back--once.
Axelrod later reran the tournament in a number of different versions, with different collections of programs. Tit-for-tat always came in near the top, and the winner was always either tit-for-tat or something very similar. Playing against itself, tit-for-tat always produces the cooperative solution--the players cooperate on every round, maximizing their combined winnings. Playing against a strategy similar to itself, tit-for-tat usually produces the cooperative solution. Axelrod reported his results in a book called The Evolution of Cooperation.
It is hard to know how seriously to take such results. They do not give the same sort of certainty as a mathematical proof, since how well a strategy does depends in part on what strategies it is playing against; perhaps some killer strategy that nobody thought of would do even better than tit-for-tat. In the first version of Axelrod's tournament, for instance, a strategy that played tit-for-tat for the first 199 moves and then betrayed on the last move would have done a little better than tit-for-tat did. In later versions the number of rounds was indefinite, with a small probability that each round would be the last, in order to eliminate such end-game strategies.
On the other hand, strategies in the real world must be adopted and followed by real people; the people submitting strategies for Axelrod's tournament were at least as clever as the average criminal defendant bargaining with the DA. And the success of tit-for-tat was sufficiently striking, and sufficiently unexpected, to suggest some new and interesting ideas about strategies in repeated games.
This sort of experiment may become more common now that computers are inexpensive and widely available. One of its advantages is that it may, as in this case, produce a striking result that would never have occurred to a game theorist, even the one setting up the experiment. Observing behavior in the real world serves the same function for economists, providing an is to check their ought to be.
Before ending this part of the chapter, I should add one important qualification. Game theory is an extensive and elaborate branch of mathematics, and not one in which I am an expert. Even if I knew enough to produce a complete description of the present state of game theory, I could not fit it into one chapter. I therefore in several places simplify the theory by implicitly assuming away possible complications. One example (in the optional section at the end of the chapter) is the assumption that one member of a coalition in a many-person game can freely transfer part of his winnings to another member. That is true if the game is three-person majority vote; it is less true if the game is the marriage market discussed in Chapter 21.
Von Neumann's analysis of many-person games considered games both with and without such side payments; my description of it will not. Readers interested in a more extensive treatment may wish to go to the book by Luce and Raiffa cited at the end of the chapter. Readers who would like to witness the creation of game theory as described by its creator should read The Theory of Games and Economic Behavior by Von Neumann and Morgenstern. It is an impressive and interesting book, but not an easy one.
You have probably realized by now that the term "game theory" is somewhat deceptive; while the analysis is put in terms of games, the applications are broader than that suggests. The first book on game theory was called The Theory of Games and Economic Behavior. Even that understates the range of what Von Neumann was trying to do. His objective was to understand all behavior that had the structure of a game. That includes most of the usual subject matter of economics, political science, international relations, interpersonal relations, sociology, and quite a lot more. In economics alone, there are many applications, but this is already a long chapter, so I shall limit myself to two: monopolistic competition and oligopoly, two quite different ways of analyzing situations somewhere between monopoly and perfect competition.
We saw in Chapter 9 that a firm in a competitive industry--a price taker--would produce where marginal cost was equal to price, and that, if the industry was open, firms would enter it until profit was driven down to zero. In Chapter 10, we saw that a single price monopoly--a price searcher--would produce where marginal cost was equal to marginal revenue, and might receive monopoly profit.
We will now consider the interesting and important case of an industry made up of price-searching firm with open entry. The condition P = MC does not hold, but the zero-profit condition does. The situation is called monopolistic competition. It typically occurs where different firms produce products that are close but not perfect substitutes. A simple example is the case of identical services produced in different places. We will start by working through one such case in some detail, then go on to see how the results can be generalized.
Figure 11-4 shows part of a long street with barbershops distributed along it. The customers of the barbershops live along the same street; they are evenly distributed with a density of 100 customers per block. Since all of the barbers are equally skilled (at both cutting hair and gossiping), the only considerations determining which barbershop a customer goes to are how much it costs and how far it is from his home. The customers are all identical, all of them get their hair cut once a month, and all regard walking an extra block to a barbershop and back again as equivalent to $1; they are indifferent between going to a barber N blocks away and paying him a price P or going to a barber N + 1 blocks away and paying P - $1.
Consider the situation from the standpoint of barbershop B. Its nearest competitors, A and C, both charge the same price for a haircut: $8. A is located eight blocks west of B; C is located eight blocks east of him. How does B decide what price to charge?
Figure 11-4
The street of barbers. There is one
barbershop every eight blocks.
Suppose he also charges $8. In that case, the only difference among the barbershops, so far as the customers are concerned, is how close they are; each customer goes to whichever one is closer. Anyone living west of point x will go to barbershop A, anyone between x and y will go to B, and anyone east of y will go to C. From x to y is eight blocks, and there are 100 customers living on each block, so barbershop B has 800 customers--and sells 800 haircuts a month.
Suppose barber B raised his price to $12. A customer at point v is two blocks from B and six from A. Since a walk of a block and back is equivalent to him to a $1 price difference, the two barbershops are equally attractive to him; he can either walk 6 blocks and pay $8 or walk 2 blocks and pay $12. For any customer between v and B, B is the more attractive option; the shorter walk more than balances the higher price. The same is true for any customer between B and w. There are four blocks between v and w, so at the higher price, B has 400 customers.
Similar calculations can be done for any price between $16 (no customers) and zero; every time B raises his price by a dollar he loses 50 customers to A and 50 to C. Figure 11-5 shows the relation between the price B charges and the number of customers he has--the demand curve for B's services. The figure also shows the corresponding marginal revenue curve and the barbershop's marginal cost, assumed constant at $4/haircut.
Looking at Figure 11-5 and applying what we learned in Chapter 10, we conclude that the barber should produce that quantity for which marginal revenue equals marginal cost; he should provide 600 haircuts a month at a price of $10 each.
So far as barber B is concerned, we seem to have finished our analysis. We know that he maximizes his profit by charging $10/haircut. The only remaining question is whether, at that price, he more than covers his total cost; to answer that we would have to know his average cost curve. If he covers total cost, he should stay in business and charge $10; if not, he should go out of business.
We are not done. So far, we have simply assumed that A and C charge $8/ haircut. But they too wish to maximize their profits. They too can calculate their marginal revenue curves, intersect them with marginal cost, and pick price and quantity accordingly. If we assume that barbershops are spaced evenly along the street and that they all started out charging the same price, then A and C started in the same situation as B--and their calculations imply the same conclusion. They too raise their price to $10--and so does every other barbershop.
How to calculate the profit-maximizing price
for a haircut. We calculate the profit-maximizing price for one
barber, assuming that adjacent barbers charge $8 for a haircut.
We are still not done. Figure 11-5 was drawn on the assumption that shops A and C were charging $8. When they raise their prices, the demand curve faced by B shifts, so $10 is no longer his profit-maximizing price.
We have been here before; the street of barbers is beginning to look very much like the egg market of Chapter 7. Once again we are trying, unsuccessfully, to find the equilibrium of an interdependent system by changing one thing at a time. Every time we get the jelly nailed solidly to one part of the wall we find that it has oozed away somewhere else.
Here, as there, we solve the problem by figuring out what the situation must look like when the equilibrium is finally reached. The analysis is more complicated than simply finding the intersection of a supply curve and a demand curve, so I shall start by sketching out the sequence of steps by which we find the equilibrium.
Each barber and potential barber must make a threefold decision: whether to be a barber, what price to charge, and where to locate his shop. His answer to those three questions defines the strategy he is following. We are looking for a set of consistent strategies: a Nash equilibrium. That means that each barber is acting in the way that maximizes his profit, given what all of the other barbers are doing.
To simplify things a little, we will start by looking for a symmetrical solution--one in which the barbershops are evenly spaced along the street and all charge the same price. The advantage of doing it this way is that if we can find an equilibrium strategy for one barber consistent with the adjacent barbers following the same strategy, we have a solution for the whole street. If we fail to find any such solution, we might have to look for one in which different barbers follow different strategies. Even if we do find a symmetrical solution, there might still exist one or more asymmetrical solutions as well; as we saw in considering which side of the road to drive on, a game may have more than one Nash equilibrium.
If the barbershops are evenly spaced and all charge the same price, we can describe the solution with two numbers--d, the distance between barbershops, and P, the price they all charge. Our problem is to find values of d and P that satisfy three conditions, corresponding to the three decisions that make up the barber's strategy. The first is that it does not pay anyone to start a new barbershop, or any old barbershop to go out of business. The second is that if all the barbers charge a price P, no individual barber would be better off charging some other price. The third is that it does not pay any barber to move his shop to a different location. If we find values of d and P for which all three conditions hold, we have a Nash equilibrium.
The first condition implies that economic profit is zero, just as for a competitive industry with open entry. The second implies the profit-maximizing condition for a price searcher: Produce a quantity such that marginal cost equals marginal revenue. We will return to the third condition later.
Figure 11-6 shows the solution. It corresponds to Figure 11-5, with three changes. I have added an average cost curve, so that we can see whether profit is positive or negative. I have set d to a value (six blocks) that results in a profit of zero. I have found a price P (=10) such that if the adjacent barbershops (A and C) are a distance d away and charge P, the profit-maximizing price for barbershop B is also P.
I have given the solution rather than deriving it, since the derivation is somewhat lengthy. Students who would like to try solving the problem for themselves should start by picking an arbitrary value of d and finding P(d), the price such that if the barbershops on either side of barbershop B are d blocks away and charge P, P is also the profit-maximizing price for B to charge. Then find Q(d), the quantity that barbershop B produces if it charges P(d). Plot P(d) against Q(d) on a graph that also shows AC as a function of quantity. The two curves intersect at a quantity and price where P=AC and profit is therefore zero, giving you the solution.
The solution--the equilibrium price of haircuts
and density of barbershops.
There is one minor flaw in our solution to the barbershop problem. We have assumed that barbershops space themselves evenly along the block. In the problem as given, there is no reason for them to do so; as you can check for yourself, barbershop B can move left or right along the street without changing the demand curve it faces. As long as it does not move past either A or C, it gains as many customers from the competitor it moves towards as it loses to the competitor it moves away from.
From B's standpoint, the situation is what I described in Chapter 7 as a metastable equilibrium. B has no reason to move and no reason not to; his situation is the same either way. If he does move, that will affect A and C; their responses will have further effects for the barbershops further along the street in both directions. If B decides to sit where we have put him--and everyone else does the same--we have a solution; if he does not, it is unclear just what will happen. So our solution is stable with regard to the first element of the strategy (whether to be a barber--the zero-profit condition) and the second (how much to charge), but only metastable with regard to the third condition (where to locate).
This problem could be eliminated by adding one more element to the situation--the customers' demand curve for haircuts. We have so far let the price charged affect which barber the customer goes to but not how often he has his hair cut; we have implicitly assumed that the demand curve for haircuts is perfectly inelastic. If we assume instead that at a higher cost (in money plus distance) customers get their hair cut less often, each barber will find that he maximizes his profit by locating halfway between the two adjacent barbers. If he moves away from that point, the number of customers stays the same but the average distance they must walk increases, so quantity demanded at any price, and the barber's profit, fall.
If the demand curve faced by a single barbershop depends not only on the location and prices of its competitors but also on the distance its customers must walk, we must redraw Figures 11-5 and 11-6. That would make the problem considerably more complicated without altering its essential logic--which is why I did not do it that way in the first place. You may, if you wish, think of Figure 11-6 as showing an almost exact solution for customers whose demand curves are almost, but not quite, perfectly inelastic. Any elasticity in the demand curve, however slight, gives the barbershops an incentive to spread themselves evenly. If the elasticity is very small, it will produce only a tiny effect on the demand curve faced by the barbershop (D), so the solution shown in the figure will be almost, although not precisely, correct.
So far, we have discussed only one example of monopolistic competition--barbershops along a street. The same analysis applies to many other goods and services for which the geographic location of seller and buyer is important--goods and services that must be transported from the producer to the consumer and those, such as haircuts or movies, for which the consumer must be transported to the producer.
Any such industry is a case of monopolistic competition, provided that firms are free to enter and leave the industry and are sufficiently far apart so that each has, to a significant degree, a captive market--customers with regard to whom the firm has a competitive advantage over other firms. This may mean that the firm can deliver its wares to those customers at a lower cost than can its more distant competitors, or it may, as in the barbershop case, mean that it costs the customers less, in time or money, to go to one firm than to another. In such a situation, the firm finds that it is a price searcher--it can vary its price over a significant range, with higher prices reducing, but not entirely eliminating, the quantity it can sell.
Firms whose product is consumed on the premises have been mentioned before--in Chapter 10. Because such firms are in a good position to prevent resale, they may also be in a good position to engage in discriminatory pricing. We could (but will not) examine the case of monopolistic competition with price discrimination; in doing so, we might produce a reasonably accurate description of movie theaters, lawyers and physicians in rural areas, private schools, and a number of other familiar enterprises.
There is another form of monopolistic competition that has nothing to do with geography or transport costs. Consider a market in which a number of firms produce similar products. An example might be the market for microcomputers. Any firm that wishes is free to enter, and many firms have done so. Their products, however, are not identical; some computers appeal more to people who have certain specific needs, certain tastes for computing style, experience with particular computers or computer languages, or existing software that will only run on particular computers. Hence different microcomputers are not perfect substitutes for each other. As the price of one computer goes up, those customers who are least locked into that particular brand shift to something else, so quantity demanded falls. But over a considerable range of prices, the company can sell at least some computers to some customers--just as a barbershop can raise its price and still retain the customers who live next door to it.
If the manufacturers of all computers appear to be making positive profits, new firms will enter the industry; if existing firms appear to be making negative profits, some will exit the industry--just as with barbershops. If one type of computer appears to be making large positive profits, other manufacturers will introduce similar designs--just as high profits on one part of the street of barbers, due to an unusually high ratio of customers to barbershops on that part of the street, would give barbershops elsewhere on the street an incentive to move closer.
Consider the recent history of the microcomputer industry. When Apple first introduced the Macintosh it was the only mass market machine designed around an intuitive, graphic, object oriented interface. In early 1985, Jack Tramiel, president of Atari, announced what was to become the Atari 520ST; the press dubbed it the "Jackintosh." At about the same time, Commodore introduced the Amiga. Over the next few years it became clear that there were a lot of customers living on that particular part of the street of computers--a lot of users who, once introduced to such a computer, preferred it to the more conventional designs. In 1988, IBM finally moved its barbershop, introducing a new line of computers (PS/2) and a new operating system (OS/2) based on essentially the same ideas.
One reason why IBM chose to move may have been that its own portion of the street was getting crowded. During the years after IBM introduced its PC, XT and AT, a large number of other companies introduced "IBM compatibles"--computers capable of running the same software, in many cases faster, and usually less expensive. By the time IBM finally abandoned the PC line, a sizable majority of IBM-compatible computers were being made by companies other than IBM.
The situation of the computer manufacturers is very similar to the situation of the barbershops--and both can be analyzed as cases of monopolistic competition. The same is true for other industries where the products of one firm are close but not perfect substitutes for the products of another (product differentiation), where some customers prefer one style of product and some another, where manufacturers are free to alter the style of their product in response to profitable opportunities, and where firms are free to enter or leave the industry.
Oligopoly exists when there are a small number of firms selling in a single market. The usual reason for this situation is that the optimal size of firm, the size at which average cost is minimized, is so large that there is only room for a few such firms; this corresponds to the sort of cost curves shown on Figure 10-10b. The situation differs from perfect competition because each firm is large enough to have a significant effect on the market price. It differs from monopoly because there is more than one firm. It differs from monopolistic competition because the firms are few enough and their products similar enough that each must take account of the behavior of all the others. The number of firms may be fixed, or it may be free to vary.
So far as their customers are concerned, oligopolies have no more need to worry about strategic behavior than do monopolies. The problem is with their competitors. All of the firms will be better off if they keep their output down and their prices up. But each individual firm is then better off increasing its output in order to take advantage of the high price.
One can imagine at least three different outcomes. The firms might get together and form a cartel, coordinating their behavior as if they were a single monopoly. They might behave independently, each trying to maximize its own profit while somehow taking account of the effect of what it does on what the other firms do. Finally, and perhaps least plausibly, the firms might decide to ignore their ability to affect price, perhaps on the theory that in the long run any price above average cost would pull in competitors, and behave as if they were in a competitive market.
Suppose all the firms decide to cooperate in their mutual benefit. They calculate their costs as if they were a single large firm, produce the quantity that would maximize that firm's profits, and divide the gains among themselves by some prearranged rule.
Such a cartel faces three fundamental problems. First, it must somehow keep the high price it charges from attracting additional firms into the market. Second, it must decide how the monopoly profit is to be divided among the firms. Third, it must monitor and enforce that division.
Preventing Entry. The cartel may try to deter entry with the threat that, if a new firm enters, the agreement will break down, prices will plunge, and the new firm will be unable to recoup its investment. The problem with this, as with most threats of retaliation, is that once the threat has failed to deter entry it no longer pays to carry it out.
The situation faced by the cartel and the new entrant can be illustrated with a payoff matrix, as shown on Figure 11-7a. All payoffs are measured relative to the situation before the new firm enters, so the bottom right cell of the matrix, showing the situation if the new firm stays out and the cartel maintains its monopoly price, contains zeros for both players.
The cartel contains ten firms and is currently making a monopoly profit of 1100. If the new firm enters the industry and is permitted its proportional share of the profit (100), the existing firms will be worse off by 100. It will cost the new firm 50 to enter the industry, so it makes a net gain of +50 (100 monopoly profit-50 entry cost) if it enters and the cartel does not start a price war (bottom left cell).
If the new firm enters and the cartel starts a price war, it loses the monopoly profit and the new firm loses its entry costs (upper left cell). If the firm does not enter and the cartel for some reason starts a price war anyway, driving prices down to their competitive level, the monopoly profit is eliminated, making the cartel worse off by 1100 (upper right cell).
Payoff matrices for a cartel and a new firm
threatening entry. Figure 11-7b shows the case where the cartel
has somehow raised entry costs; Figure 11-7c shows the case where the
cartel has raised the cost to itself of giving in.
A crucial feature of this game is that the new firm moves first; only after it enters the industry does the cartel have a chance to respond. So the new firm enters, knowing that if the cartel must choose between losing 100 by sharing its profit and losing 1,100 by eliminating it, the former option will be chosen.
How might the cartel alter the situation? One way would be to somehow increase the entrance cost above 100. The result would look something like Figure 11-7b. Staying out dominates entering for the new firm.
The simplest and most effective way of raising entrance costs is probably through government. Consider the trucking industry under Interstate Commerce Commission (ICC) regulation. In order for a new carrier to be allowed to operate on an existing route, it had to get a certificate from the ICC saying that its services were needed. Existing carriers would of course argue that they already provided adequate service. The result would be an expensive and time-consuming dispute before the commission.
Another approach to preventing entry is for the cartel somehow to commit itself--to build the economic equivalent of a doomsday machine. Suppose the ten firms in the cartel could sign legally binding contracts guaranteeing their customers a low price if an eleventh firm enters the industry. Having done so, they then point out to potential new firms that there is no point in entering, since if they do there will be no monopoly profit for anyone.
This particular solution might run into problems with the antitrust laws, although, as we will see shortly, similar devices are sometimes used by cartels to control their own members. A more plausible solution might be for the cartel members to somehow commit their reputations to fighting new entrants, thus raising the cost of giving in. By doing so they alter the payoff matrix, making it more expensive to themselves to choose the bottom left cell; doing so will destroy their reputation for doing what they say, which may be a valuable business asset. Figure 11-7c shows the case where the firms in the cartel will lose reputation worth 2000 if they give in.
Looking at the payoff matrix, it seems that the firms have only hurt themselves; they have made their payoff worse in one cell and left it the same in the others. But the result is to make them better off. The new firm observes that, if it enters, the cartel will fight. It therefore chooses not to enter. The situation is precisely analogous to the earlier cases of commitment. Just as in those cases, the player who commits himself is taking a risk that the other player may somehow misread the situation, call the bluff, and discover that it is no bluff, thus making both players worse off.
Dividing the Gains. The second problem a cartel faces is deciding how the monopoly profit is to be divided among the member firms. In doing so, it is engaged in a game similar to bilateral monopoly but with more players. If the firms all agree on a division there will be a monopoly profit to be divided; if they cannot agree the cartel breaks up, output rises, prices fall, and most of the monopoly profit vanishes.
Here again, the cartel may attempt to defend itself by the equivalent of a doomsday machine--a commitment to break up entirely and compete prices down to marginal cost if any firm insists on producing more than its quota. How believable that threat is will depend in part on how much damage the excess production does. If Algeria decides to increase its oil production from 1 percent to 2 percent of total OPEC output, the threat by Saudi Arabia to double its production in response and eliminate everyone's profit, its own included, may not be taken very seriously. Figure 11-8 shows the corresponding payoff matrix. As before, all payoffs are measured relative to the initial situation.
FIGURE 11-8
Payoff matrix showing the consequence of output
increases by Saudi Arabia and Algeria.
One great weakness of a cartel is that it is better to be out than in. A firm that is not a member is free to produce all it likes and sell it at or just below the cartel's price. The only reason for a firm to stay in the cartel and restrict its output is the fear that if it does not, the cartel will be weakened or destroyed and prices will fall. A large firm may well believe that if it leaves the cartel, the remaining firms will give up; the cartel will collapse and the price will fall back to its competitive level. But a relatively small firm may decide that its production increase will not be enough to lower prices significantly; even if the cartel threatens to disband if the small firm refuses to keep its output down, it is unlikely to carry out the threat.
So in order for a cartel to keep its smaller members, it must permit them to produce virtually all they want, which is not much better than letting them leave. The reduction in output necessary to keep up the price, and the resulting reduction in profits, must be absorbed by the large firms. In the recent case of the OPEC oil cartel, it appears that the reduction of output has been mostly by Saudi Arabia and the United Arab Emirates. One consequence is that it is the Saudis who are the most reluctant to have OPEC raise its price, since it is they who pay in reduced sales for any resulting reduction in the quantity demanded.
Enforcing the Division. The cartel must not only agree on the division, it must somehow monitor and enforce the agreement. Each member has an incentive to offer lower prices to favored customers--mostly meaning customers who can be lured away from other firms and trusted to keep their mouths shut about the deal they are getting. By doing so, the firm covertly increases its output above the quota assigned to it, and thus increases its profit. Such behavior destroyed many of the attempts by railroad companies to organize cartels during the nineteenth century--sometimes within months of the cartel's formation.
A number of devices may be adopted to to prevent this. One is for all members of the cartel to sell through a common marketing agency. Another is for the firms to sign legally binding contracts agreeing to pay damages to each other if they are caught cheating on the cartel agreement. Such contracts are neither legal nor enforceable in the United States, but they are in some other countries.
Another and more ingenious solution is for all of the member firms to include a Most-Favored-Customer clause in their sales contracts. Such a clause is a legally binding promise by the seller that the purchaser will get as low a price as any other purchaser. If a firm engages in chiseling--selling at below the official price to some customers--and is eventually detected, customers that did not get the low price can sue for the difference. That makes chiseling a very expensive proposition unless you are sure you will not get caught, and thus helps maintain the stability of the cartel.
Figure 11-9 shows the payoff matrix for a two-firm cartel before and after the firms add Most-Favored-Customer clauses to their sales contracts. Before (Figure 11-9a), the firms are caught in a prisoner's dilemma; the equilibrium outcome is that both of them chisel. After (Figure 11-9b), the cost of chiseling has been increased, making it in both firms' interest to abide by the cartel price. Just as in the case shown by Figure 11-7c, the firms have made their alternatives less attractive, lowering the payoffs in some of the cells, and have benefited themselves by doing so.
Figure 11-9
Payoff matrices for a two-firm cartel, before
and after adding a Most-Favored-Customer clause. The clause
raises the cost of chiseling to either firm, changing the dominant
strategy from the lower right cell (both firms chisel) to the upper
left (both firms abide by the cartel agreement).
There are many other contractual devices that can be used by a cartel to control cheating by its members. A Meet-or-Release clause is an agreement by which a seller guarantees that if the customer, after agreeing to buy, finds a lower price elsewhere, the seller will either meet the price or release the customer from his agreement. Such a clause gives the customer an incentive to report chiseling by other firms, in order to get a low price for itself; it thus makes such chiseling more risky and less profitable.
A particularly elegant device for controlling cheating is cross licensing of patents. Suppose there are two firms in the widget industry, each with a variety of patents covering particular parts of the production process. Each firm can, if it wishes, produce widgets without infringing the other firm's patents. Instead, the firms cross license; each agrees that, in exchange for permission to use the other firm's patents, it will pay the other firm $10 for every widget it produces.
The effect of the agreement is to raise marginal cost for each firm by $10/widget. At the higher marginal cost, each firm finds it in its interest to produce less. If their combined output is still too high, they raise the licensing fee and continue doing so until output reaches the profit-maximizing level--the level that would be produced by a single monopoly firm.
The beauty of this solution is that as long as the licensing fee is paid, there is no need for each firm to check on what the other firm is doing. It is in the private interest of each firm, given that it must pay the license fee, to keep its output down. Average cost is unaffected by the fee, assuming the firms produce the same amount, since each receives as much as it pays. But marginal cost is raised by the amount of the fee, and it is marginal cost that determines output.
There is at least one more way that a cartel may try to control its members--by turning itself into a monopoly. If the firms in the cartel merge, many of the cartel's problems disappear. The disadvantage of merging is that it may raise costs; presumably the reason there were several firms initially instead of a single natural monopoly was that the efficient scale for a firm was less than the full size of the market. That is a price the individual firms may be willing to pay, if in exchange they get to sell at a monopoly price without worrying about chiseling by other members of the cartel or threats by some members to pull out unless they receive a larger share of the market.
Of course, in forming the merger, there is still a bargaining problem; the owners of each firm want to end up with as large a fraction as possible of the new monopoly's stock. It may be hard for each firm to judge just how much it can ask for its participation in the merged firm. When J.P. Morgan put together U.S. Steel, one crucial step was buying out Andrew Carnegie for $400 million dollars. Morgan is said to have commented later that if Carnegie had held out for $500 million, he would have paid it.
One problem that merger does not eliminate is the problem of entry by new firms. Indeed, it may increase that problem. Threats by one large firm to increase output and drive down prices if a new firm enters are even less believable than threats by a group of firms, for the same reason that the Saudis are in a weak position in bargaining with Algeria or Venezuela. And if the larger firm has higher costs than the new entrant, its position is weaker still. When U.S. Steel was put together in 1901, its market share was about 61%. By 1985 it was down to 16%.
I have discussed a variety of different devices that cartels use to control cheating by their members. Such cheating is a bad thing from the standpoint of the cartel's members, but a good thing from the standpoint of the rest of us--their customers. This raises the question of why devices such as Most-Favored-Customer clauses and cross licensing of patents are not illegal.
The general issue of regulating monopolies will be discussed at some length in Chapter 16. For the moment, it is sufficient to point out that all of these devices may also be used for other purposes. A Most-Favored-Customer clause may be a way of guaranteeing the customer that he will not be the victim of price discrimination by a supplier in favor of his competitors. A cross licensing agreement may permit firms to lower their costs by each taking advantage of the other's technology. It is easy enough for me, writing a textbook, to assume that the widget firms can each produce widgets just as well using only its own patents, but there may be no easy way for a court to determine whether that is true for real firms in a real industry. A merger may be intended to give the new firm a monopoly at the expense of a higher production cost, but it may also be a way of lowering production costs by combining the different strengths of several different firms.
This does not, of course, mean that the government makes no attempt to regulate such behavior. Mergers between large firms have often been the target of antitrust suits. One problem is, as I suggested in the previous chapter, that such intervention may do more harm than good. While it may make it more difficult for oligopolies to charge monopoly prices, it may also make it more difficult for new firms to form that would compete with existing monopolies. A second problem is that, for reasons that will be discussed in Chapter 19, it may often be in the interest of the government doing the regulation to support the producers against their customers rather than the other way around.
. . . the high price for the crude oil resulted, as it had always done before and will always do so long as oil comes out of the ground, in increasing the production, and they got too much oil. We could not find a market for it . . . of course, any who were not in the association were undertaking to produce all they possibly could; and as to those who were in the association, many of them men of honor and high standing, the temptation was very great to get a little more oil than they had promised their associates or us would come. It seemed very difficult to prevent the oil coming at that price.--John D. Rockefeller, discussing an unsuccessful attempt to cartelize the production of crude oil. Quoted in McGee, op.cit.
Rockefeller was too pessimistic; there is a way of keeping a high price from drawing more oil out of the ground. The solution is a monopoly in the original sense of the term--a grant by government of the exclusive right to produce.
Consider the airline industry. Until the recent deregulation, no airline could fly a route unless it had permission from the Civil Aeronautics Board. The CAB could permit the airlines to charge high prices while preventing new competitors from entering and driving those prices down. From the formation of the CAB (originally as the Civil Aeronautics Administration) in 1938 until deregulation in the late 1970s, no major scheduled interstate airline came into existence.
Even if the airlines, with the help of the government, were able to keep out new firms, what prevented one airline from cutting its fares to attract business from another? Again the answer was the CAB; under airline regulation it was illegal for an airline to increase or reduce its fares without permission. The airline industry was a cartel created and enforced by the federal government, at considerable cost to the airlines' customers.
In order for a private cartel to work, the number of firms must be reasonably small; otherwise the smaller firms will correctly believe that an expansion in their output will increase their sales with only a negligible effect on price. That is not true for a governmentally enforced cartel. The government can provide protection against both the entry of outsiders and expanded output by those already in the industry, thus providing an industry of many small price-taking firms with monopoly profits--at the expense of its customers. If the government prevents entry but does not control output, we have one of the situations discussed in Chapter 9--a competitive industry with closed entry.
One form such arrangements often take is professional licensing. The government announces that in order to protect the public from incompetent physicians (morticians, beauticians, poodle groomers, egg graders, barbers, . . .), only those with a government-granted license may enter the profession. Typically the existing members of the profession are assumed to be competent and receive licenses more or less automatically. The political support for the introduction of such arrangements comes, almost invariably, not from the customers, who are supposedly being hurt by incompetent practitioners, but from the members of the profession. That is not as odd as it may seem; the licensing requirement makes entry to the profession more difficult, reducing supply and increasing the price at which those already in the profession can sell their services.
In discussing the problems a cartel faces, I have so far ignored the element of time. Supply curves are usually much less elastic in the short run than in the long. If the price of oil rises sharply, it may be years before the additional investment in exploration and drilling generated by the opportunity to make high profits has much effect on the amount of oil being produced. The same is true for demand. In the short run, we can adjust to higher oil prices by taking fewer trips, driving more slowly, or lowering our thermostats. In the medium run, we can form carpools. In the long run, we can buy smaller and more fuel-efficient cars, live closer to our jobs, and build better insulated homes.
So even if a cartel can succeed in raising the price--and its profits--for a few years, in the long run both the price and the cartel's sales are likely to fall as customers and potential competitors adjust. In the case of OPEC, the process of adjustment was somewhat delayed by the Iran-Iraq war--during which the combatants reduced each other's petroleum output by blowing up refineries, pipelines, and ports.
So far we have been considering outcomes in which the firms in an oligopolistic industry agree to cooperate, although we have assumed that each will violate the agreement if doing so is in its interest. An alternative approach is to assume that the oligopoly firms make no attempt to work together. Perhaps they believe that agreements are not worth making because they are too hard to enforce, or that there are too many firms for any agreement to be reached. In such a situation, each firm tries to maximize its profit independently. If each firm acts independently, the result is a Nash equilibrium.
Part of the definition of Nash equilibrium is that each player takes what the other players are doing as given when deciding what he should do; he holds their behavior constant and adjusts his to maximize his gains. But if one firm increases its output, the other firms must adjust whether they choose to or not. If they continue to charge the same price, they will find that they are selling less; if they continue to produce the same amount, the price they can sell it for will fall. The firms, taken together, face a downward-sloping demand curve, and there is no consistent way of assuming it out of existence.
This means that, in describing the game, we must be careful what we define a strategy to be; as you will see, different definitions lead to different conclusions. The two obvious alternatives are to define a strategy by quantity or by price. In the former case, each firm decides how much to sell and lets the market determine what price it can sell it at; in the latter, the firm chooses its price and lets the market determine quantity. We will try to find the Nash equilibrium for an oligopoly first on the assumption that a firm's strategy is defined by the quantity it produces and then on the assumption that it is defined by the price the firm charges.
Strategy as Quantity--Version 1. On this interpretation of Nash equilibrium, each firm observes the quantities being produced by the other firms and calculates how much it should produce to maximize its profit, assuming that their output stays the same. Figure 11-10 shows the situation from the standpoint of one firm. D is the demand curve for the whole industry. Qother is the combined output of all the other firms in the industry. Whatever price the firm decides to charge, the amount it will sell will equal total demand at that price minus Qother; so Df, D shifted left by Qother, is the residual demand curve, the demand curve faced by the firm. The firm calculates its marginal revenue from that, intersects it with marginal cost, and produces the profit-maximizing quantity Q*.
We are not quite finished. If the situation is a Nash equilibrium, then not only this firm but every firm must be producing the quantity that maximizes its profit, given the quantities produced by the other firms. If all firms are identical, then all firms will find the same profit-maximizing output. On Figure 11-10, Qother is eight times Q*, so the situation is a Nash equilibrium provided there are exactly nine firms in the market. Each firm produces Q*, so from the standpoint of any one firm there are eight others, with a total output of Qother=8Q*.
One firm in an oligopoly calculates its
profit-maximizing quantity of output where marginal revenue equals
marginal cost. Marginal revenue is calculated from the residual
demand curve Df. Other firms are assumed to hold the
quantity they produce constant.
We have not yet considered the possibility of new firms entering the industry in response to the opportunity to make above-market profits. If entry is forbidden by law, we can forget that problem. But if anyone who wishes can start a new firm with the same cost curves as the old one, there is one more step to finding equilibrium. With nine firms, price is above average cost, so profit is positive. Redo the problem with ten firms; if price is still above average cost, try eleven. When you reach a number of firms for which price is below average cost, you have gone too far; if the number is twelve, then in equilibrium there will be eleven firms. The twelfth will not enter because it knows that if it does it, along with the existing firms, will make negative profits.
We are now back at something very much like monopolistic competition--marginal cost equal to marginal revenue and profit (approximately) equal to zero. The one difference is that we are assuming all firms produce identical products, so Firm 1 is just as much in competition with Firm 12 as with Firm 2.
Version 2--Reaction Curves. Another way of solving the same problem is in terms of reaction curves--functions showing how one firm behaves as a function of the behavior of the other firms. The more firms in the industry, the more dimensions we need to graph such functions. Since we have only two dimensions available, we will consider the simple case of duopoly--an industry with two firms. This is, as it happens, the case analyzed by Cournot, who invented the fundamental idea more than a century before Nash.
Figure 11-11 shows the situation from the standpoint of one of the firms. D is the demand curve for the industry. D1 is the residual demand curve faced by Firm 1, given that Firm 2 is producing a quantity Q2=40; D1 is simply D shifted left by Q2. Q1 is the quantity Firm 1 produces, calculated by intersecting the marginal revenue curve calculated from D1 with the firm's marginal cost curve MC1.
By repeating this calculation for different values of Q2, we generate RC1 on Figure 11-12--the reaction curve for Firm 1. It shows, for any quantity that Firm 2 chooses to produce, how much Firm 1 will produce. Point A is the point calculated using Figure 11-11. The same analysis can be used to generate RC2, the reaction function showing how much Firm 2 will produce for any quantity Firm 1 produces. Since the two firms are assumed to have the same cost curves, their reaction curves are symmetrical. The Nash equilibrium is point E on Figure 11-12. At that point and only at that point, each firm is producing its optimal quantity given the quantity the other firm is producing.
Calculating one point on firm 1's reaction
curve. If Firm 2 produces Q2=40, Firm 1 maximizes its
profit by producing Q1=13
Suppose the firms start instead at point A. Firm 1 is producing its optimal quantity (13) given that Q2 is 40, but 40 is not the optimal quantity for Firm 2, given that Q1 is 13. So Firm 2 shifts its output to put it on its reaction curve at point B. Now its output is optimal, given what Firm 1 is doing. But Firm 1 is no longer on its reaction curve; 13 units is not its optimal output, given what Firm 2 is now doing, so Firm 1 increases Q1, moving to point C.
As you can see, the two firms are moving closer and closer to point E. In Chapter 7, we saw that the point where a downward-sloped demand curve crosses an upward-sloped supply curve is a stable equilibrium: if prices and quantities are moved away from that point, they tend to come back. We have just shown that the same thing is true for the reaction curves of Figure 11-12.
The disadvantage of this approach to finding the equilibrium as compared to the first approach we used is that while reaction curves make mathematical sense for any number of firms, it is hard to graph them for more than two. The advantage is that this approach can be applied to a much wider range of problems. We have applied it to a situation where strategy is quantity produced. It could just as easily be applied to two firms each picking a location at which to build its store, or two political parties each choosing a platform and a candidate, or two nations each deciding how many missiles to build. In each case, the reaction curve shows what strategy one player chooses, given the strategy of the other. Nash equilibrium occurs where the two curves intersect, since only there are the strategies consistent--each optimal against the other.
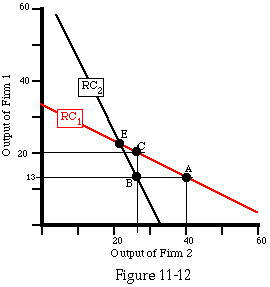
Using reaction curves to find a Nash
equilibrium. E, where the two curves cross, is the equilibrium
point. Starting at A, firm 2 would reduce its output in order to get
to its reaction curve at B. Firm 1 would then increase its output,
moving to C. The sequence moves the system towards E, showing that
the equilibrium is stable.
Strategy as Price. We will now redo the analysis of oligopoly with one small change--defining a strategy as a price instead of a quantity. Each firm observes the prices that other firms are charging and picks the price that maximizes its profit on the assumption that their prices will not change.
Since all of the firms are producing identical goods, only the firm charging the lowest price matters; nobody will buy from any other. Figure 11-13 shows the situation from the standpoint of one firm. Pl is the lowest of the prices charged by the other firms.
The firm in this situation has three alternatives, as shown by Df. It can charge more than Pl and sell nothing. It can charge Pl and sell an indeterminate amount--perhaps Q(Pl)/N, if there are N firms each charging Pl. It can charge less than Pl, say one penny less, and sell as much as it wants up to Q(Pl). It is easy to see that the last choice maximizes its profit. It is facing the horizontal portion of the demand curve Df, so the quantity it sells (up to Q(Pl), which on this figure is more than it wants to sell) does not affect the price. It maximizes its profit by producing Q* and selling it for just under Pl.
We are not yet done; in a Nash equilibrium, not only this firm but every firm is maximizing its profit. That is not what is happening here. Each other firm also has the option of cutting its price, say by two cents, and selling all it wants. Whatever price the other firms are charging, it is in the interest of any one firm to charge a penny less. The process stops when the price reaches a level consistent with each firm selling where price equals marginal cost. If there are enough firms, or if additional identical firms are free to enter the industry, the process stops when price gets down to minimum average cost, at which point each firm is indifferent between selling as much as it likes at that price and selling nothing at all.
One firm in an oligopoly chooses its
profit-maximizing price. All other firms are assumed to hold
their prices constant; the lowest such price is P1. The
firm maximizes its profit producing Q* and selling it for just under
P1.
Bertrand Competition. Oligopolistic firms that produce where price equals marginal cost, just as if they were in a competitive industry, are engaged in Bertrand competition. This seems a peculiar thing to do if we define an oligopoly as a market where the individual firm is large enough so that its output has a significant effect on price. Firms are assumed to maximize their profit; they do so, as we saw in the previous chapter, by producing the quantity for which marginal revenue equals marginal cost. If the firm's output affects price then marginal revenue is below price, so it intersects marginal cost at a lower quantity, so the firm produces less than the competitive output.
Bertrand competition is less unrealistic if we define oligopoly as a market with only a few firms. In some such markets, the firm may be able to affect price only in the very short run. If there are lots of other firms that can easily enter the industry--and will if price is high enough to make doing so profitable--the situation may be equivalent to a competitive market.
We have just seen another possible explanation of Bertrand competition. If firms believe that other firms react to them by holding price constant and varying output, they end up producing the quantity for which price equals marginal cost, just as in a competitive market.
The Hand is Quicker than the Eye. We are now just about finished with the enterprise of using Nash equilibrium to analyze oligopoly. In order to describe a Nash equilibrium, we must define a strategy. We have considered two alternative definitions, one in which a firm picks a quantity to sell and one in which it picks a price to sell at. We have shown that those two definitions produce two quite different predictions for what the firms will end up doing--how much they will produce and what the price will be.
We could, if we wished, continue the process using more complicated strategies. Perhaps we could find a third solution to oligopoly, and a fourth, and a fifth. But there is not much point in doing so. We already have two answers to one question, and that is enough. More than enough.
I hope I have convinced you that game theory is a fascinating maze. It is also, in my judgment, one that sensible people avoid whenever possible. There are too many ways to go, too many problems that have either no solution or an infinite number of them. Game theory is very useful as a way of thinking through the logic of strategic behavior, but as a way of actually doing economics it is a desperation measure, to be used only when all easier alternatives fail.
Many mathematical economists would disagree with that conclusion. If one of them were writing this chapter, he would assure you that only game theory holds out any real hope of introducing adequate mathematical rigor to economics, that everything else is a tangle of approximations and hand waving. He might concede that game theory has not produced very much useful economics yet, but he will assure you that if you only give him enough time wonderful things will happen.
He may be right. As you have probably gathered by now, I have a high opinion of John Von Neumann. When picking problems to work on, ones that defeated him go at the bottom of my list.
Although the only solution concept for a many-person game used in the chapter was the Nash equilibrium, a variety of other solutions have been derived by game theorists and used by economists. Two of the more important are the Von Neumann stable set and the core.
Consider a fixed-sum game played by n players. Suppose that, after some negotiation, a group of m of them decide to ally, playing to maximize their combined return and then dividing the gains among themselves by some prearranged rule. Further suppose that the remaining players, observing the coalition, decide to cooperate in their own defense, and also agree to some division of what they can get among their members.
We have now reduced our n-person game to a two-person game--or rather, to a large number of different two-person games, each defined by the particular pair of coalitions playing it. Since fixed-sum two-person games are, in principle, a solved problem, we may replace each of them by its outcome--what would happen if each coalition played perfectly, as defined by the Von Neumann solution to the two-person game.
We now have a new n-person game--coalition formation. Each coalition has a value--the total winnings its members will receive if they play together against everyone else. How much each player ends up getting depends on what coalitions are formed and on how the coalition of which he is a member agrees to divide up its combined take. Three-person majority vote, which we discussed earlier, is an example of a simple coalition game; the value of any coalition with two (or three) members is $100, since a majority could allocate the money. The value of a coalition with one member is zero.
Von Neumann defined an imputation as a possible outcome of the game, defined by how much each player ended up with. An imputation X was said to dominate another imputation Y if there was a group of people all of whom were better off with X than with Y and who, if they formed a coalition, could guarantee that they got X. In other words, X dominates Y if:
i. There is some coalition C such that X is a better outcome than Y for everyone in C (each person gets more), and
ii. The value of C, the combined winnings that the members of C will get if they cooperate, is at least as great as the amount that X allocates to the members of C.
We have now stated, in a more formal way, the ideas earlier applied to three-person majority vote. We may express the imputations in that game in the form (a,b,c), where a is the amount going to Anne, b to Bill, c to Charles. The imputation (50,50,0) means that $50 goes to Anne, $50 to Bill, and nothing to Charles.
Suppose we start by considering the imputation (50,50,0). It is dominated by the imputation (60,0,40), since Anne and Charles are both better off under the new division and their two votes are enough to determine what happens. The imputation (60,0,40) is in turn dominated by (0,50,50), and so on in an endless cycle. This is the sequence of bargains discussed for this game in Part 1.
Von Neumann tried to solve this problem by defining the solution to a many-person game not as a single imputation but as a group of imputations (called a stable set) such that within the group no imputation dominated another and every imputation outside of the group was dominated by one inside. One Von Neumann solution to three-person majority vote is the set of imputations:
(50,50,0),(50,0,50),(0,50,50)
It is fairly simple to show that no one of them dominates another and that any other imputation is dominated by at least one of them.
There are, however, some problems with this definition. To begin with, the solution is not an outcome but a set of outcomes, so it tells us, at most, that some one of those outcomes will occur. It may not even tell us that; there is no reason to assume that one game has only one solution. Three-person majority vote in fact has an infinite number of solutions, many of which contain an infinite number of imputations!
Consider the set of imputations (x,100-x,0), 0<= x<= 100. It contains an infinite number of separate imputations, each defined by a different value of x. Examples are (10,90,0), (40,60,0), and (4.32,95.68,0), corresponding to x=10,40, and 4.32. It is simple to show that this set is also a solution; none of the infinite number of imputations within it is dominated by another, and every imputation outside the set is dominated by one inside the set.
Put in words, this solution corresponds to a situation where Anne and Bill have agreed to cut Charles out of the money and divide it between themselves in some one of the infinite possible ways . This is called a discriminatory solution; Charles is the victim of the decision by Anne and Bill to discriminate in favor of themselves and against him. There are lots of such discriminatory solutions, each containing an infinite number of imputations. They include two more in which one player is cut out entirely, plus an infinite number in which one player is given some fixed amount between zero and 50 and the other two divide the rest between themselves in all possible ways.
You may by now have concluded that Von Neumann's definition of a solution to the many-person game is more confusing than useful, since it may, and in this case does, generate an infinite number of solutions, many (in fact an infinite number) of which each contain an infinite number of outcomes. If so, I agree with you; Von Neumann's solution is a gallant try, but unlike his solution to two-person games it does not tell us much about the outcomes of games, even games played by perfect players with infinite calculating ability.
Before going on to discuss other solution concepts, it is worth pausing for a moment to see what Von Neumann did and did not accomplish. In analyzing two-person fixed-sum games, he first showed that all such games could be reduced to one--a matrix of outcomes, with each player choosing a strategy and the outcome determined by the intersection of the two strategies. He then solved that game. Within the limits of his definition of a solution, we now know how to solve any two-person fixed-sum game, although we do not happen to have enough computing power actually to solve any save very simple ones.
In analyzing many-person games, Von Neumann followed a similar strategy. He first showed that all such games could be reduced to one--a game in which players negotiate to form coalitions and divide the resulting gains, against a background defined simply by how much each coalition, if formed, can win. That is as far as he got. He failed to find a solution to that negotiation game that is of any real use in understanding how people do or should play it.
The Core. If you think that conclusion is evidence against my earlier description of John Von Neumann as one of the smartest people in this century, I suggest you try to produce a better definition for a solution to a many-person game. Many people have. The solution concept currently most popular with economists who do game theory is a somewhat different one, also based on Von Neumann's work. It is called the core, and is defined as the set containing all imputations not dominated by any other imputation.
The core has two advantages over the Von Neumann solution. First, since it is defined to contain all undominated imputations, it is unique; we do not have the problem of choosing among several different cores for the same game. Second, since imputations in the core are undominated, once you get to one of them you may plausibly be expected to stay there; there is no proposal by the losers that can both benefit them and lure enough of the winners away to produce a new winning coalition. But while the core is unique, it may contain more than one imputation, so it still does not tell you what the outcome will be.
Furthermore, there is no guarantee that the core will contain any imputations at all. Three-person majority vote has no undominated imputations; whatever outcome is agreed upon, there is always some new proposal that benefits two of the players at the expense of the third. One of the things that economists who use game theory do is to prove whether the game describing a particular hypothetical economy does or does not have an empty core --whether there are any undominated imputations. This turns out to be closely related to the question of whether there is a competitive equilibrium for that economy.
1. Some games, including Scissors, Paper, Stone, are often played by children for negative stakes; the winner's reward is to be permitted to slap the loser's wrist. It is hard to see how such behavior can be understood in economic terms. Discuss what you think is going on, and how you would analyze it economically.
Figure 11-14
Cost curves for an avocado farm, problem 4.
2. Birds (and other animals) compete for scarce food. When two birds find the same piece of food, each has the choice to fight or to flee. If only one is willing to fight, he gets the food at no cost. If neither is willing to fight, each has a 50 percent chance that the other will start running first, leaving him with the food. If both fight, each has a 50 percent chance of getting the food but also some chance of being injured.
Suppose there are two varieties of a species of bird, differentiated only by their willingness to fight; in all other ways they are identical. The "hawk" variety always fights; the "dove" always flees. The two live in the same environment. Whichever variety on average does better at food gathering will tend to increase in numbers relative to the other.
Getting a piece of food is worth a gain of 10 calories. If a hawk fights another hawk over a piece of food, the damage is on average the equivalent of -50 calories. Draw the corresponding payoff matrix.
a. In equilibrium, what are the relative numbers of hawks and doves"
b. Explain why.
c. What part of the chapter does this problem relate to? Explain.
3. Suppose that having an aggressive personality pays; almost all of the time other people back down and give you what you want. What do you think will happen to the number of people who adopt that strategy? What will be the effect of that on the payoff to the strategy? Discuss.
4. Figure 11-14 shows marginal cost and average cost for an avocado farm; it also shows demand, D, for avocados. Answer each question first on the assumption that a strategy is defined as a quantity and again on the assumption that it is defined as a price.
a. Firms can freely enter the avocado industry. In Nash equilibrium, how many firms are there, what is the price, what is the quantity? What is the profit for each firm?
b. There are two avocado farms; no more are permitted. In Nash equilibrium what is the price, what is the quantity? What is the profit for each firm?
5. The game of matching pennies is played as follows. Each player puts a penny on the table under his hand, with either the head or the tail up. The players simultaneously lift their hands. If the pennies match (both heads or both tails), Player A wins; if they do not match, Player B wins.
a. Figure 11-15a shows the payoffs. Is there a Von Neumann solution? What is it? What is the value of the game?
b. Figure 11-15b shows a different set of payoffs. Answer the same questions.
c. If the players both picked heads or tails at random, they would break even under either set of payoffs. Does this imply that both sets of payoffs are equally fair to both players? Discuss.
Figure 11-15
Payoff matrices for the game of matching
pennies, problem 5.
6. There are two firms in an industry; industry demand (D) and firm cost (MCf, ACf) curves are as shown in Figure 11-10. The firms decide to control output by cross-licensing. What fee should they charge to maximize their profit:
a. Assuming that they will end up in a Nash equilibrium with strategies defined as quantities?
b. Assuming that they will engage in Bertrand competition?
7. The level of noise at a party often gets so loud that you have to shout to make yourself heard. Surely everyone would be better off if everyone kept his voice down. Discuss the logic of the situation from the standpoint of the ideas of this chapter.
8. Apply the idea of monopolistic competition to a discussion of the market for economics textbooks, with particular reference to this one.
The plot of Doctor Strangelove was apparently borrowed from the novel Red Alert by Peter George (writing under the pseudonym Peter Bryant). In many ways, the novel gives the more interesting version. The air force officer who launches the attack is a sympathetic character, an intelligent and thoughtful man who has decided that a preemptive strike by the United States is the only way out of a trap leading eventually to surrender or mutual destruction. He arranges the attack in such a way that only he can cancel it, notifies his superiors, pointing out that since they cannot stop the attack they had better join it, and then commits suicide. The one flaw in his plan is that the Russians have built a doomsday machine.
At several points in this chapter, I have described the player of a game as choosing a strategy, giving it to a computer, and watching the computer play. There is in fact at least one computer game that works just that way. It is an old game for the Apple II called Robot War. The players each program an imaginary robot, then watch their robots fight it out on the computer screen, each following his programming. Not only is it a concrete example of one of the abstractions of game theory, it is also a brilliant device for using a computer to teach programming; when your robot loses, you figure out why and modify your program accordingly.
My description of how a computer can be used as a metaphor for bounded rationality is based on a talk I heard by Ehud Kalai on his recent work, some of which is described in the paper by Kalai and Stanford listed below.
For a discussion of strategic behavior, the original source is John Von Neumann and Oskar Morgenstern, Theory of Games and Economic Behavior (Princeton: Princeton University Press, 1944). An easier introduction is R. Duncan Luce and Howard Raiffa, Games and Decisions: Introduction and Critical Survey (New York: John Wiley & Sons, 1957).
An original set of essays on strategic problems is Thomas Schelling, The Strategy of Conflict (Cambridge: Harvard University Press, 1960).
Other works of interest are:
Robert Axelrod, The Evolution of Cooperation, NY: Basic Books, 1984.
E.H.Chamberlin, The Theory of Monopolistic Competition. Cambridge, MA Harvard University Press, 1933.
A. Cournot, Researches into the Mathematical Principles of the Theory of Wealth, NY: Macmillan & Co., 1897. This is a translation of a book originally published in French in 1838.
H. Hotelling, "Stability in Competition," Economic Journal, 39 (Mar. 1929):41-57.
Ehud Kalai and William Stanford, "Finite Rationality and Interpersonal Complexity in Repeated Games," Econometrica 56(1988), 397-410 .
John F. Nash Jr., "Non-cooperative Games," Annals of Mathematics 54(1951), 289-95 .
J. Robinson, The Economics of Imperfect Competition. London: Macmillan, 1933.
P. Sraffa, "The Laws of returns under competitive conditions," Economic Journal 36(1926), 535-50
[This is some additional material that was cut from the published
version of the chapter to save space.]
In thinking about the game of bilateral monopoly, it may have occurred to you that there is a simple and obvious solution. There is a dollar to be divided, so let the two players split it fifty-fifty.
This is one example of an idea introduced into game theory by Thomas Schelling, and called after him a Schelling point. The essential idea is that players may converge on an outcome not because it is fair, not because it is somehow determined by players following the correct strategy, but because it is unique. If we add to our description of bilateral monopoly or three-person majority vote the realistic assumption that bargaining costs something, since it uses up time and energy that could be spent doing something else, a Schelling point seems a possible solution. As long as each proposal can be followed by another and equally plausible one, it is hard to see how the process can stop. A proposal that seems special simply because it is somehow unique, such as an even split, may seem attractive to everyone simply as a way to end the argument.
It is tempting to interpret this as a situation where ethical ideas of fairness are determining the outcome, but it is probably a mistake. One can easily imagine cases where two bargainers agree on a fifty-fifty split even though neither thinks it is fair. And one can apply the idea of a Schelling point to games where fairness is simply irrelevant.
Consider the following simple example. Two players are separately given a list of numbers and told that they will receive a hundred dollars each if they independently choose the same one. The numbers are:
2, 5, 9, 25, 69, 73, 82, 100, 126, 150
Each player is trying to find a number that the other will also perceive as unique, in order to maximize the chance that they both choose the same one. No issues of fairness are involved, but the solution is a Schelling point if one exists.
What the solution will be depends very much on who the players are. Non-mathematicians are likely to choose 100, since to them it seems a particularly unique number. Mathematicians will note that the only special thing about 100 is that it is an exact square, and the list contains two other exact squares, so 100 is not a unique choice. They may well converge on 2, the only even prime and thus a very odd number indeed. To a pair of illiterates, on the other hand, 69 might seem the obvious choice, because of its peculiar symmetry.
The same observation, that the Schelling point is in part a feature of the game and in part a feature of how the players think about the game, applies to bilateral monopoly as well. Suppose the players are from some culture where everyone believes that marginal utility is inverse to income--if your income is twice as great as mine you get half as much utility from an additional dollar as I do. It might occur to them that since it is utility and not money that really matters, the natural division of a dollar is the division that gives each player the same utility. To them, a fifty-fifty split would be a split in which each player's share was proportional to his income.
For these reasons, it is hard to convert Schelling's insight into a well defined theory. Nonetheless, it is an interesting and often persuasive way of looking at games, especially bargaining games, that seem to have no unique solution and yet somehow, in the real world, get solved.